Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 7

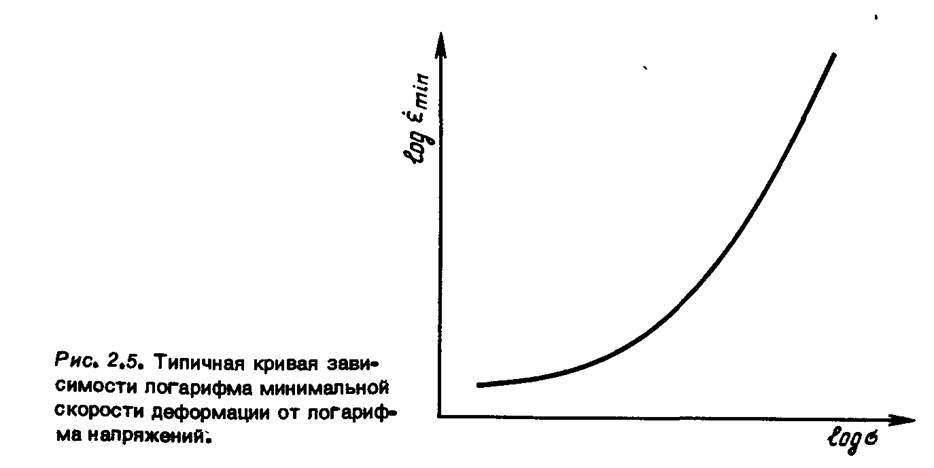
Рис, 2.5. Типичная кривая зави­симости логарифма минимальной скорости деформации от логариф­ма напряжений;

tog 6

стр42

22

Глава 2.Феноменологическое описание ползучести

2.1. Явление ползучести

23

Ч)

-Г

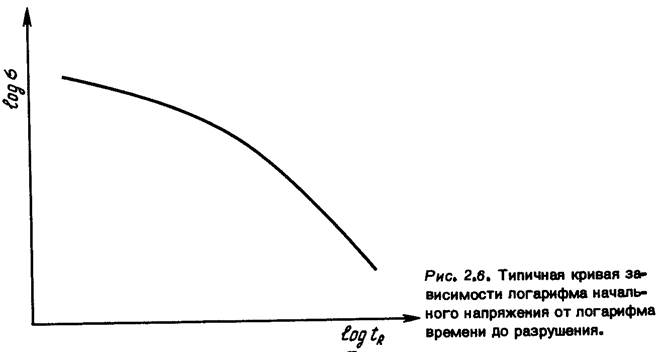
Рис. 2.6. Типичная кривая за­висимости логарифма началь-. ного напряжения от логарифма времени до разрушения.

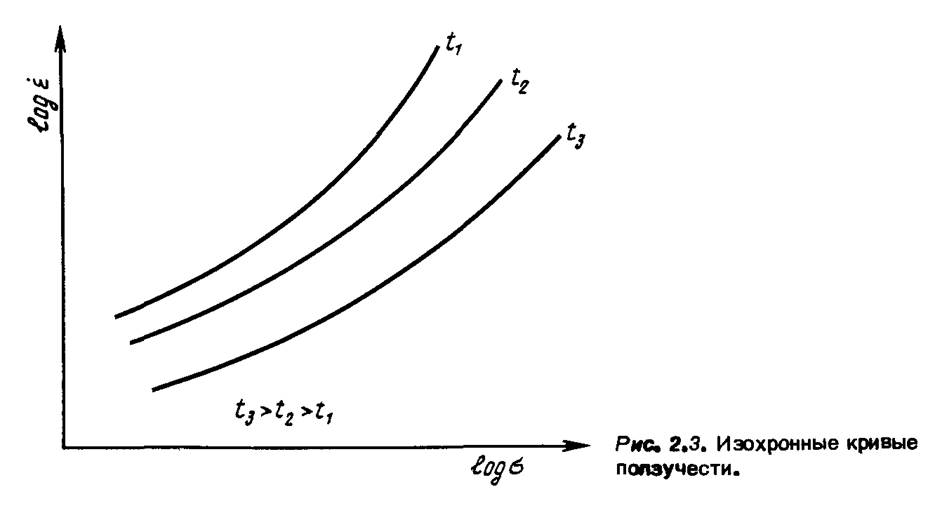
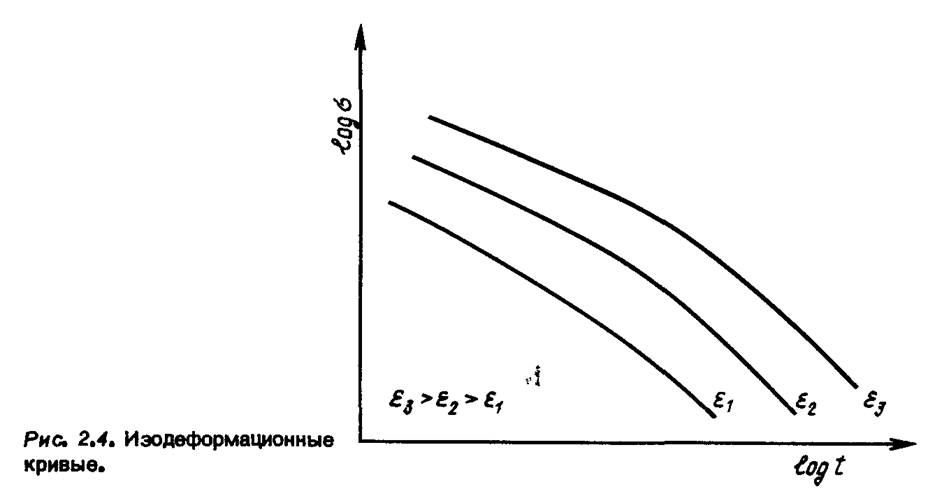
типа на некоторых участках можно приблизительно считать прямыми (с по­ложительным углом наклона) — это означает, что минимальная скорость ползучести является степенной функцией напряжений, однако в эксперимен­тах с уменьшением нагрузки угол наклона обычно уменьшается. Анализи­руя зависимость напряжений от времени до разрушения, можно предполо­жить, что время до разрушения обратно пропорционально некоторой степен­ной функции напряжений, однако в экспериментах с более длительными временами также происходит изменение угла наклона (показателя -степени). В ранних работах часть-кривой, отличающаяся малым временем и высоким уровнем напряжений, связывалась с хрупким разрушением; в настоящее время установлено, что хрупкий характер разрушения имеет место при ма­лых деформациях. Поскольку природа ползучести такова, что определение ее характеристик требует значительного времени, то естественно, что ин­женеры-проектировщики стремятся экстраполировать результаты кратко­временных испытаний на длительные времена или на другие уровни нагруз­ки. Однако - как можно усмотреть из кривых на рис. 2.5 и 2.6 - такая экстраполяция наталкивается на значительные трудности.

Мы можем без труда учесть те сложности, которые могут возникать из-за меняющейся во времени нагрузки или температуры. В частности, лег­ко можно оценить влияние изменения температуры на основе следующих соображений. Если мы нарисуем кривую зависимости минимальной скорос­ти ползучести от температуры (рис. 2.7), то можно видеть, что скорость ползучести экспоненциально растет с ростом температуры, и, следователь­но, даже небольшое изменение температуры может привести к удвоению скорости ползучести! (Эта экспоненциальная зависимость представляет собой проявление хорошо известного закона Аррениуса, который ввиду его

Г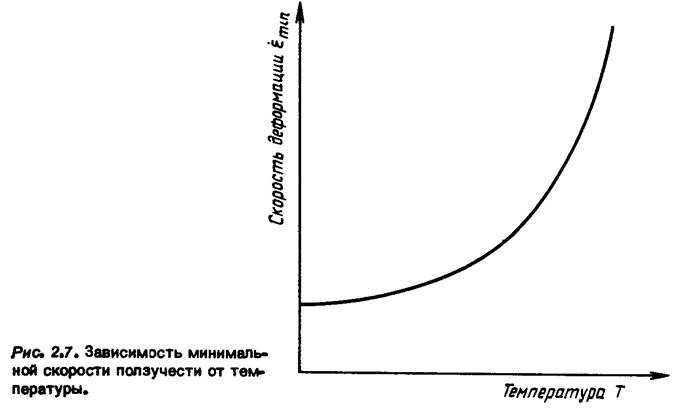

•<и

I I

Рис* 2.7. Зависимость минималь­ной скорости ползучести от тем­пературы.

Температура Т

общности применим не только к описанию ползучести металлов, но и к дру­гим физическим и биологическим процессам.)

Простейшим примером с непостоянной нагрузкой является эксперимент, при котором удлинение образца поддерживается постоянным, вследствие чего происходит уменьшение (релаксация) нагрузки (рис. 2.8). Явление ре­лаксации в металлах обычно хорошо предсказывается по результатам опы­тов с постоянной нагрузкой (хотя для некоторых материалов типа полиме­ров это не так). В случае меняющейся нагрузки некоторое представление

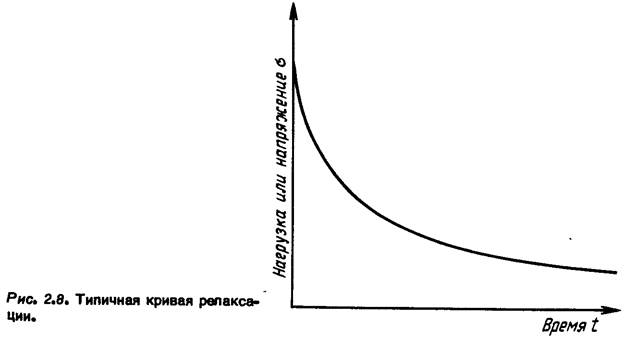
Рис» 2.8. Типичная кривая релакса­ции.

Время t

24

Глава 2.Феноменологическое описание ползучести

Время!

Время t

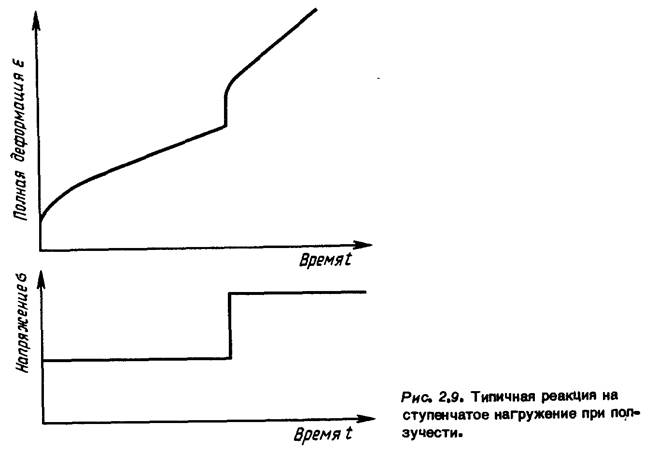
Рис, 2,9. Типичная реакция на ступенчатое нагружение при пол­зучести.

Разгрузка

Упругий возврат

Постоянная деформация

Время t

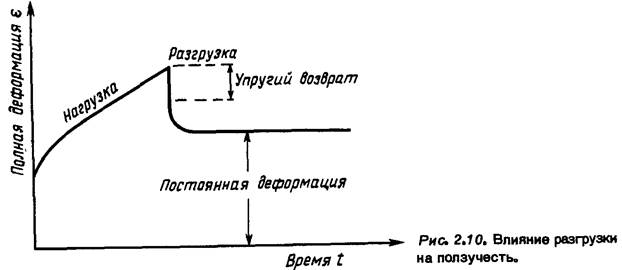
Рмс, 2,10. Влияние разгрузки на ползучесть.

о сложности поведения материала, обладающего способностью к ползучес­ти, можно получить с помощью анализа результатов опыта при ступенча­том нагружении(рис. 2.9) и опыта с частичной разгрузкой (рис. 2.10), в ко­тором обнаруживается явление обратной ползучести. При циклической на­грузке, являющейся комбинацией этих видов нагрузок, приходим, таким образом, к весьма сложной картине, и ясно, что из результатов экспери­ментов с постоянной нагрузкой нельзя извлечь адекватную модель ползу­чести, материала.

2.2. Физические механизмы ползучести

25

В заключение этого раздела следует подчеркнуть, что гладкие кривые типа показанных на рисунках в эксперименте получить нельзя вследствие разброса  экспериментальных данных, полученных в разных экспериментах. Разброс обусловлен не только неидентичностью образцов в пределах одной партии, но и чувствительностью деформаций ползучести к малым измене­ниям температуры и нагрузки. Таким образом, в опытах на ползучесть до­пуски на измеряемые параметры должны быть весьма малыми, что на прак­тике трудно осуществить.