На рис. 9.6 приведены зависимости времени полного разрушения от нагрузки для некоторых типичных значений материальных констант; видно, что эта зависимость в логарифмических координатах очень близка к линейной.
9.4. ТЕОРИЯ РАЗРУШЕНИЯ СПЛОШНОЙ СРЕДЫ
Итак, возникла необходимость выяснить, каков же полный эффект накопления повреждений и распространения разрушения в сплошной среде. Аналог данного эффекта мы наблюдали, хотя и в очень скрытой форме, в рассмотренной выше задаче о разрушении многостержневой системы. При разрушении очередного' стержня мы имели дело с задачей для новой конструкции, исследование которой было достаточно простым. Если же речь идет о теле под нагрузкой, то из определяющих уравнений должно вытекать, каким образом в каждой точке тела будут связаны между собой напряжения, скорости деформаций и поврежденность. Поскольку в разных точках тела уровни напряжений различны, то в соответствии с этим будут различаться и степени поврежденности. Определяющие уравнения в данной точке будут применимы до того момента, пока здесь не будет выполнен соответствующий критерий разрушения. Начиная с этого момента частица материала в рассматриваемой точке тела не в состоянии выдерживать нагрузку и, следовательно, разрушается. С течением времени область разрушенного материала увеличивается до тех пор, пока конструкция больше не сможет выдерживать приложенную извне нагрузку и полностью выходит из строя. Этот процесс можно описать следующим образом. Рассмотрим тело, занимающее область Vс границей S, нагруженное внешними усилиями и закрепленное некоторым образом (рис. 9.7). До момента времени, который мы будем обозначать через tj, разрушенных подобластей в теле нет. Как и в случае многостержневой сис'Ллы, назовем эту стадию скрытым разрушением (или ин-
262
Глава 9.Разрушение при ползучести
Разрушенный материал
Фронт разрушения
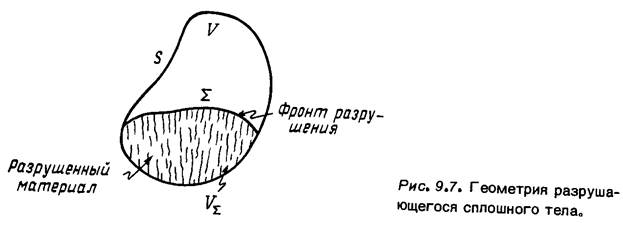
рис. 9.7. Геометрия разрушающегося сплошного тела.
кубационным периодом). В момент времени <г некоторая частица (или подобласть) разрушается, и мы назовем данный момент моментом начала разрушения. Далее поверхность 2, отделяющая разрушенную и неразрушенную зоны, будет продвигаться по телу. Эта движущаяся поверхность называется фронтом разрушения. Движение фронта разрушения будет продолжаться До момента времени t^ , когда конструкция полностью выходит из строя. Период времени от момента «г до гп называется периодом распространения разрушения.
Описанная здесь проблема разрушения континуума отличается от тех, с которыми обычно сталкиваются в механике сплошных сред. Для формулировки и последующего решения соответствующих краевых задач необходимо проследить за движением фронта разрушения. Для того чтобы отличать этот новый класс задач от рассмотренных нами ранее, мы назовем данный класс механикой (теорией) разрушения сплошной среды.
9.4.1. Математическая формулировка теории разрушения сплошной среды
Для построения математической формулировки теории обратимся к формализму, развитому в разд. 7.3. В качестве основы будем использовать задачу Коши для деформаций ползучести (разд. 7.3.5), реализуя высказанные в предыдущем разделе (при обсуждении задачи о многостержневой системе) соображения.
Рассмотрим сплошное тело, занимающее область Vс поверхностью 5, нагруженное объемными силами; к части поверхности тела приложены поверхностные силы, а на остальной части заданы перемещения. Предполагается, что материал при таких внешних воздействиях повреждается: в момент времени <j в некоторой точке начнется разрушение, после чего фронт разрушения будет продвигаться по телу (рис. 9.7) до момента времени «1Г, тогда конструкция полностью выйдет из строя. Область, занятую разрушенным материалом, обозначим через V^; очевидно, что и положение фронта разрушения, и область F2 являются функциями времени. Рассмотрим отдельно две стадии процесса разрушения.
9.4. Теория разрушений сплошной среды
263
9.4.1.1, Стадия скрытого разрушения: П ^ t ^ tl
На этой стадии материал не разрушается, хотя поврежденность его растет. Процесс накопления деформаций ползучести е£ можно описать при помощи следующей задачи Коши:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.