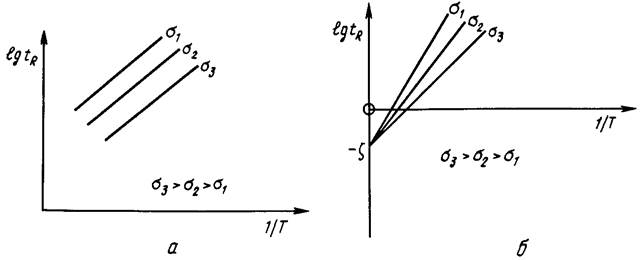
Подобный метод применим в том случае, когда графики зависимости 1§«й от обратного значения абсолютной температуры 1/7 при фиксированном напряжении представляют собой семейство параллельных прямых (в соответствии с уравнением (П. 8)). На практике экспериментальные данные могут не удовлетворять данному ограничению, т.е. вести себя не так, как показано на рис. 11. 8, в, а иметь тенденцию сойтись и пересечься в некотором фокусе (рис. 11.8, б). В последнем случае из соотношения (11.8) следует вывод о том, что комбинация lg(<4/C/(o-)) не зависит от напряжений (и равна, скажем, £), в то время как параметр Д# меняется при изменении напряжений. Следовательно, для установления корреляции с напряжениями нужно использовать параметр
Р2=
tgt,
 б
б
Рчс, 11,8, Зависимость времени до разрушения от обратной величины температуры для различных значений напряжения.
314
Глава 11.Проектирование конструкций с учетом ползучести
Введенные здесь параметры /J и Р2 представляют собой примеры целой группы так называемых температурно-временных параметров, Цель введения которых — сжать семейство кривых разрушения в одну кривую, позволяющую осуществить экстраполяцию. Исчерпывающий обзор затронутого вопроса можно найти в книге Конвея [ 24], более поздние результаты — в обзорных статьях [ 25,26].
Отметим, что параметр Р1 предложен в работах Орр — Шерби и Дорна, Р2 — работах Ларсона и Миллера. Большинство подходов к решению поставленной проблемы основано на предположении, что существует единственная функциональная зависимость между временем до разрушения, напряжением и температурой, которая может быть записана в виде Р{ Т, tR) = { (у). Очень часто принимается более частное предположение о том, что реализуется соотношение Р(Т, tR) = Glga, температурно-временной параметре котором равен
(П.9)
Здесь А - постоянная, р(Т) - заданная функция температуры; в частности, при использовании параметра Орр — Шерби — Дорна pj имеем
А= 0,
Отметим, что большинство известных температурно-временных зависимостей можно преобразовать к форме (11.9) [27]. Вопрос состоит в том, какой из температурно-временнйх параметров выбрать; как установлено на практике, не существует одного раз и навсегда зафиксированного параметра, который был бы пригоден для всех материалов. Некоторое представление о тех проблемах, с которыми здесь приходится сталкиваться, можно получить, анализируя данные Мэнсона и Хаферда [28], приведенные на рис. 11.9, а. На этом рисунке показаны эталонные кривые разрушения нержавеющей стали (18%Сг — 8%), построенные с использованием параметра Ларсона — Миллера, причем для всех вариантов приведены две осредненные кривые, первая из которых получена по результатам кратковременных испытаний (менее 100 ч), вторая — длительных. Видно, что результаты длительных опытов плохо согласуются с результатами экстраполяции по осредненной кривой кратковременных испытаний. Такой же вывод вытекает из анализа обычно используемых кривых зависимости напряжений от времени разрушения (рис. 11.9,6). Стоит отметить, что, как видно из рис. 11.9, а, отклонения от срединной кривой являются систематическими, что в^жою очередь ставит под вопрос законность использования для данного материала гипотезы о линейности связи lg tR с параметром 1/Г.
Для преодоления возникших затруднений был предложен [ 29] подход, рекомендуемый в качестве стандартного: процедура должна автоматически выбирать наилучший для данного материала температурно-временнбй параметр. Например, если для исследуемого материала наилучшим является параметр Орр — Шерби — Дорна им же Ларсона - Миллера, то конечный результат должен иметь соответствующую форму; если лучшим оказывается какой-либо другой параметр, процедура должна его
11.1.Моделирование поведения материала при проектировании
315
°922,CttК о 917,59 К «1033,2 К * 1088,7 К. К х 1255,4 К
Кривая, coomoemcmSy-ющая Временам За разрушения * ЮОч шеванные значки
Средняя кривая Всем дан-
Сплошные кривые соответствуют временам до разрушения & 100'ч
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.