Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 15

в котором индексом Т обозначена операция транспонирования (и, следователь­но, е ^то означает скалярное произведение векторов; напомним, что мы исполь­зуем матричную символику).

Граница тела, подлежащая дискретизации

Отдельный элемент Узел

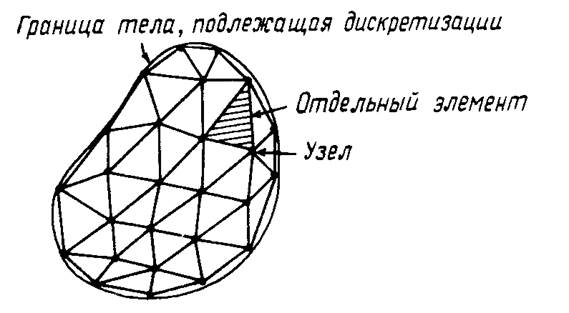
рис, 7.16, Дискретизация сплош­ного тела по методу конечных элементов.

206

Глава 7. Анализ напряжений при неустановившейся ползучести

Используя соотношения (7.29) и (7.32), преобразуем выписанное уравне­ние к следующей форме:

a^T\f_y([L][N])^TodV-

-f   [N]^TpdS \ = О,

Р

откуда следует, что выражение в фигурных скобках равно нулю, т.е. / [B]^TodV - F=0. Здесь введены обозначения

[B] = [L\[N], F = / [N]^TbdV+ f  [N}^TpdS.

^SP

Подставляя определяющие соотношения (7.30) и (7.31), получим уравнение

[K]a-F_c-F = 0,                                                            (7.33)

в котором определены матрица жесткости

(K]-f_y[B]^T(D][B]dV

и вектор усилий, обусловленных ползучестью,

F_c = f_r[B]^T[D]t_cdV.

Уравнения для процесса перераспределения напряжений выводятся следую­щим образом. Записав соотношения (7.30), (7.31) и (7.32) в скоростной форме, находим равенство

подставляя в которое решение уравнения (7.33), получаем

Используя теперь определяющее уравнение теории ползучести, например, в виде ё_с = / (а, f), получим следующее уравнение для задачи Коши:

— (, -e°) = [D]fB][K]-¹(J (B]^T[D]f(o,t)dV)-[D]f(o,t],         (7.34) dtV

в котором о° = [D][fl][*:]~¹F - эквивалентное упругое напряжение. Из по­следнего соотношения вытекает начальное условие

«(0)-в°(0).                                                                                             (7.35)

которое полностью определяет требуемую задачу Коши.

Сосредоточим теперь внимание на проблеме разыскания конечного мно­жества значений а., i= 1, 2, ..., G, в G точках интегрирования внутри об­ласти V. Объемные интегралы будем вычислять при помощи квадратурной формулы

? */<*»),-

7.6. Метод конечных элементов

207

конкретный вид которой пока не фиксируем. ^Отметим лишь, что весовые ко­эффициенты c_kположительны.

Обозначая через а. , [В. ] значения а и [В] в точках интегрирования г = 1, 2, ..., G, из уравнения (7.34) получим систему

—в. =[ОПВ.][КГ'( 2  c,[B.]^T[D]f(et))-[D]f(o;, t) + *,°,

dt    '7=1

i-1,2.....G.                           (7.36)

Аналогичную систему уравнений можно вывести и для процесса измене­ния неупругих деформаций е   .  Не останавливаясь на подробных выкладках, приведем лишь результат

_!-•     ./([Й^ККГ¹   2  c[B]^T[0-]_V-[D]e_a. +a,°.t), dt                               j= i                 '

i =1, 2.....G.                      (7.37)

Построить аналитическое решение уравнений (7.36) или (7.37) для практичес­ки интересных задач, как правило, невозможно, и обычно для их решения при­меняют численные алгоритмы. Ниже мы опишем два таких алгоритма.

7.6.1 Явная схема Эйлера

Из всех существующих схем численного интегрирования наибольшее рас­пространение в методе конечных элементов (применительно к пошаговому ре­шению задач теории ползучести) получила, по-видимому, схема Эйлера. Реали­зуется данная схема следующим образом:

1. Строится решение исходной упругой задачи, в котором формируют­ся вектор F и матрица [К]~¹ . Полагая е_с|. = 0 во всех уанах интег­рирования, вычисляют

2. Вычисляется шаг по времени At, и из определяющего уравнения

вычисляются значения ё    :

3. Определяются приращения деформаций ползучести

4. Формируются векторы fh f_c, где

ГЛАВА 8

ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧ   ТЕОРИИ НЕУСТАНОВИВШЕЙСЯ   ПОЛЗУЧЕСТИ