Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 29

304

Глава 11.Проектирование конструкций с учетом ползучести

исходные данные по ползучести были преобразованы путем логарифмирова­ния; следовательно, если v ? — дисперсия данных до преобразования (пред­полагаемая постоянной), то, как нетрудно проверить, дисперсия данных пос­ле преобразования будет равна

1

IdE     \

»I-----------I

U-J

1

Таким образом, даже в том случае, когда веса исходных данных постоянны (и, следовательно, их можно считать равными единице), веса преобразован­ных данных а>Т = [ё _с (i)]².

Для иллюстрации высказанных соображений была дана оценка коэффи­циентов В и л поданным, приведенным в табл. 11.1, путем минимизации выражений (11.2), (11.5) с весами, равными единице, а также с весами, вы­численными по приведенной выше формуле. Результаты вычислений сведе­ны в табл. 11.2; наиболее важный и очевидный вывод состоит в том, что результаты существенно различаются, особенно для коэффициента В. Воп­рос о том, какое значение считать наилучшим — найденное на основании исходных данных или по данным после преобразования, — не является закон­ным, поскольку (это следует напомнить и подчеркнуть) "наилучшее соответ­ствие" было обеспечено только для одного частного критерия — минимума суммы квадратов ошибок.

Таблица 11.1. Данные по установившейся ползучести нержавеющей

стали марки 316 при 1300°Г (977,59 К), приведенные в работе [бб]

и/6,895, МПа	«с*103, ч"1	ст /6, 895, МПа	£Сх103, ч"1	ст/6,895, МПа	£СхЮ3, ч"1
6	0,0038	13,19	0,096	23,20	2,30
6	0,0044	13,19	0,085	23,20	3 20
7	0,0079	15,49	0,17	25,20	5,80
7	0,0069	15,49	0,26	25,20	5,10
9,55	0,027	18.63	0,37	29,52	14,70
9,55 11,23	0,025 0,080	18,63 21,38	0.49 1,40	29,52	27,36
11,23	0,055	21,38	1,20

Таблица 77.2. Оценка параметров

Невзвешенный метод наимень­ших квадратов (преобразован­ные данные)

Взвешенный метод наименьших квадратов(преобразованные данные)

Нелинейный метод наименьших квадратов (исходные данные)

4.78-Ю-²⁵    5,06

1,61-10~³⁸   8,07 1,21.10~³⁷  7,87

11.1.Моделирование поведения материала при проектировании

305

Можно, разумеется, использовать и Другие крите­рии ; например можно было бы минимизировать сумму квадратов "обратных значений"

/-1/

a))i²,

или среднеквадратичную "ошибку" S       5Д

D=

Здесь

¹(с с (i-)).

Применение указанных альтернативных критериев подчеркивает различие в характере установившейся ползучести на различных участках кривой ползу­чести (рис. 11.1) и приводит к различным оценкам констант.

Выбор подходящего критерия — в руках исследователя. По этому поводу добавим только, что в случае, когда количество подлежащих определению ма­териальных констант велико, а принятые определяющие соотношения сущест­венно нелинейны, реализация метода наименьших квадратов может натолкнуть­ся на большие затруднения, и необходимо обратиться ко второму методу - ме­тоду "косвенной идентификации".

О  т

Среднеквадратичное откло­нение

.данные эксперимента — Кривая, найденная по методу

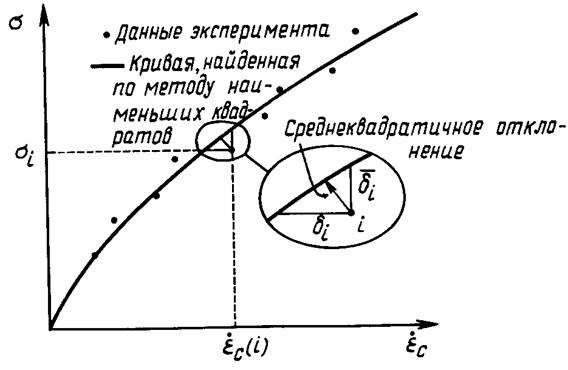
Рис. 11.1. Графическое представление метода наименьших квадратов.

65

306

Глава 1 ^Проектирование конструкций с учетом ползучести

1 1. 1.2.2. Косвенная идентификация

Метод косвенной (непрямой) идентификации наиболее часто применяет­ся при моделировании поведения материала и идентификации в теории пол­зучести. Особо важную роль этот метод играет в теориях с внутренними па­раметрами состояния, когда определяющие соотношения содержат ненаблюда­емые величины. Метод не является стандартным, и для его; реализации в каждом конкретном случае нужна дополнительная работа; характеризовать его лучше всего как метод последовательного исключения параметров, за­висящий от структуры принятых определяющих соотношений. Приведем два примера.