Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 31

Очевидным недостатком подхода, используемого нами до этого момента, является то, что экспериментальные данные могут оказаться неполными. На­пример, могут отсутствовать данные о деформации ползучести; кривые, ха­рактеризующие разрушение при ползучести, могут быть получены для ограни­ченных пределов изменения напряжения и температуры и т.д. И, как всегда приходится иметь дело с разбросом параметров. Для того чтобы иметь воз­можность проанализировать напряжения в некоторой конструкции, изобрета­ется наиболее подходящая, но тем не менее приближенная математическая модель поведения материала; исследователь поневоле вынужден довольство­ваться такой аппроксимацией. По этой причине во многих методах проектиро­вания обращение к анализу ползучести происходит на конечном этапе проек­тирования. Например, проект может быть основан просто на проверке дости­жения пределов упругости, и, если пределы упругости не достигаются, целост­ность конструкции на протяжении всего заданного периода ее эксплуатации будет обеспечена (и тем самым отпадает необходимость обращения к этой книге). В качестве альтернативы можно применять метод базисных напряже­ний (гл. 5, разд. 9.7), который автоматически связывает поведение исследу­емого элемента конструкции с характеристиками ползучести материала. Уро­вень напряжений, полученных при реализации любого из этих подходов, мо­жет выйти за пределы исследованной нами области (что ни в коей мере не является неожиданным, поскольку в действительности нужны эксперименты по ползучести, длительность которых сравнима с проектным периодом экс­плуатации). Для преодоления этих затруднений необходимо научиться уверен­но экстраполировать имеющиеся данные на область высоких значений напря­жений и температуры. Однако, если данных для экстраполяции мало (как это часто имеет место в отношении деформаций ползучести), одного умения экс­траполировать может оказаться недостаточно для решения проблемы. Жела­тельно уметь также коррелировать данные по деформации ползучести с бо­лее доступными данными по разрушению. Методы корреляции и экстраполя­ции сходны; рассмотрим сначала проблему корреляции.

11.1.3.1. Корреляция данных по разрушению и деформированию

Отметим прежде всего, что вторая и третья стадии ползучести не неза­висимы — каждая из них представляет собой неотъемлемую часть единого процесса ползучести. Отсюда вытекает, что должна существовать явная за­висимость между точкой разрушения и предшествующим участком стандарт­ной кривой ползучести (хотя, конечно, нет никаких оснований предполагать, что такая зависимость будет простым алгебраическим соотношением).

Если обратиться к стандартной кривой ползучести (рис. 11.4), то нетруд­но видеть, что минимальная скорость ползучести может быть определена из формулы e_min = (s₄ — e j)/«/{ • Следовательно, в том случае, когда величи­на Е₄- ej  не зависит от напряжений, существует обратно пропорциональ­ная зависимость минимальной скорости ползучести от времени до разруше­ния. Установлено [ 16], что данная зависимость на самом деле реализуется для многих металлов; улучшить отмеченную корреляцию можно путем введе­ния еще одной константы, когда вместо выписанного выше соотношения име-

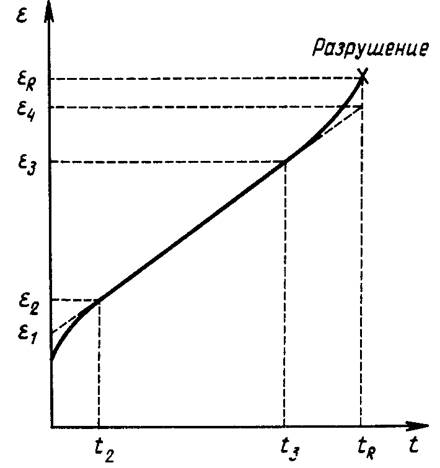
Рис. 11.4, Стандартно» ползучести.

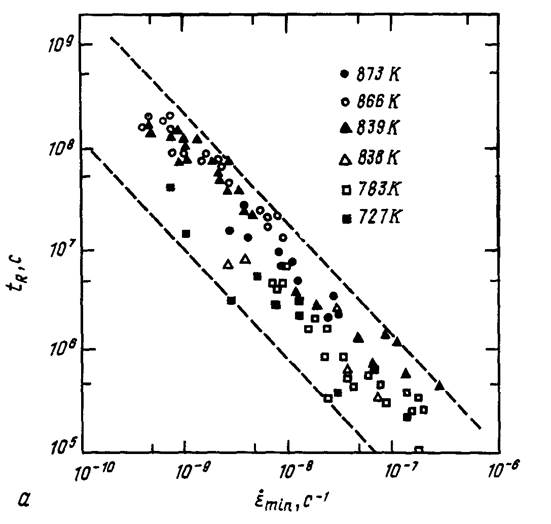
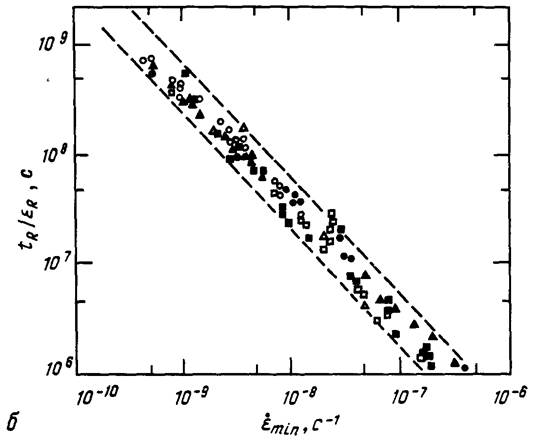
pmc, 11.5, Зависимости времени до разрушения (а) и отношения времени до разруше­ния к деформации в момент разрушения (б) от минимальной скорости ползучести (см. работу [ 19]. рис. 1(>) и 1(в)).

11.1. Моделирование поведения материала при проектировании

311

ем (в логарифмических координатах) [ 17]

lgi

= С.

(11.6)

Здесь т и С - константы. На практике величина т очень близка к едини­це. Соотношения, аналогичные (П.6), хорошо выполняются для многих ме­таллических сплавов, однако для некоторых из них параметры т и С ока­зываются зависящими от напряжения и температуры. Был предложен [ 18] улучшенный вариант соотношения (11.6), в котором отмеченная зависимость (от напряжения и температуры) меньше: