Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 6

Задачи, которые мы приводим в этой книге, подобраны таким образом, чтобы читатель мог воспроизвести их решение самостоятельно. Численные решения (которые, вообще говоря, нужны и которых могло бы быть больше), требующие применения специализированных программ для ЭВМ, в книге от­сутствуют. Разумеется, читателю, имеющему некоторые навыки програм­мирования и знающему методы вычислений, работать будет легче. (В настоя­щее время существует много учебников по программированию и методам вычислений, которые читатель может использовать в своей работе; мы осо­бенно рекомендуем книгу Конта и Бура [29].) Может, однако, случиться так, что расчетчику понадобятся универсальные конечно-элементные программы, в которых предусмотрен учет ползучести материала. Сейчас в обращении находится немало хороших программных комплексов; ниже мы перечислим

2. ФЕНОМЕНОЛОГИЧЕСКОЕ ОПИСАНИЕ   ПОЛЗУЧЕСТИ

2.1   ЯВЛЕНИЕ ПОЛЗУЧЕСТИ

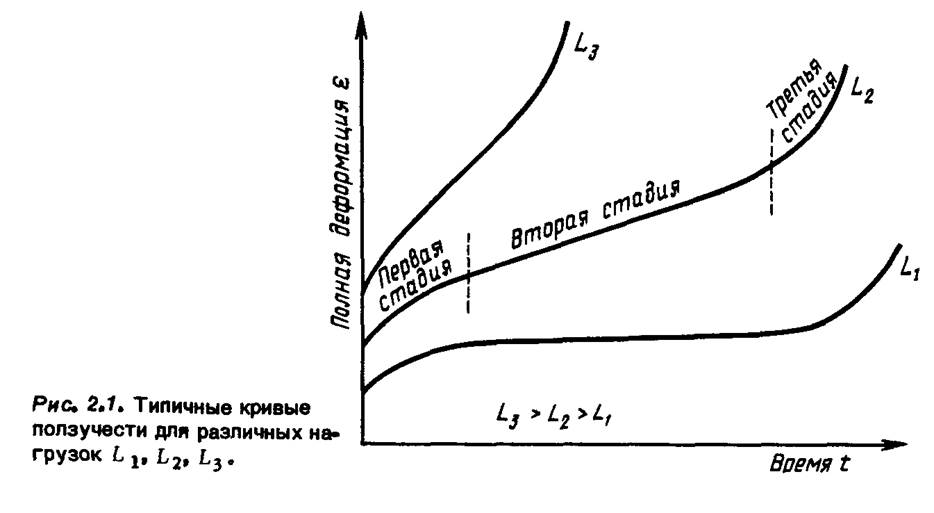
Мы начнем с рассмотрения, что происходит в образце при одноосном растяжении, когда нагрузка в течение некоторого промежутка времени остается постоянной, а температура высока настолько, что вызывает пол­зучесть. Типичные кривые зависимости деформации от времени приведены на рис. 2.1. Заметим, что, если мы повторим эксперимент при другом зна­чении нагрузки (перейдем от L, к L_s), результат может оказаться совер­шенно иным. Полученная кривая состоит из качественно различных участ­ков. Во-первых, существует начальный линейно-упругий участок, который не зависит от скорости нагружения (временно мы не будем рассматривать случаи, когда нагрузка настолько велика, что возникают мгновенные плас­тические деформации). Далее на кривой ползучести можно выделить три участка: участок с уменьшающейся скоростью ползучести, обусловленный так называемой первичной ползучестью (или первой стадией); участок с при­близительно постоянной скоростью ползучести, связанный со второй стади­ей или состоянием установившейся ползучести; участок с возрастающей скоростью ползучести, относящийся к третьей стадии ползучести. Эти опре-деления становятся более прозрачными, если мы обратимся, к кривой зави­симости скорости деформации от времени (рис. 2.2). На первой и Второй стадиях ползучести эксперимент идет при постоянном напряжении.Однако

Рис. 2.J. Типичные кривые ползучести для различных на­грузок L_t. lj, L.

L₃>L₂>t.,

время t

20

Глава 2.Феноменологическое описание ползучести

I

I

g

I

Пердая стадия

Вторая стайия

Третья стадия

рис. 2.2. Типичная кривая за-

________^. висимости скорости деформа-

Время tции от времени.

на третьей стадии увеличение скорости деформации в значительной степе­ни обусловлено изменением площади поперечного сечения вследствие на­копленных деформаций. Кроме того, разрушение материала из-за возникно­вения внутренних пор также может изменить эффективное поперечное се­чение, воспринимающее внешнюю нагрузку. Следовательно, описание тре­тьей стадии ползучести требует особой осторожности.

Информация, содержащаяся в основных кривых ползучести, может быть представлена в различных формах, каждая из которых позволяет наи­более четко пояснить ту или иную ситуацию. Для практики наиболее полез­ны две из этих форм - изохронные кривые (или просто изохроны), рис. 2.3, и изодеформационные кривые (кривые постоянных деформаций), рис. 2.4.

-»~    Рис. 2,3. Изохронные кривые ползучести.

2.1. Явление ползучести

21

Ч>

Рис. 2.4. Иэодеформационные кривые.

В ранних работах по теории ползучести использовались кривые зависимос­ти логарифма скорости деформации от логарифма напряжение для фиксиро­ванного момента времени - этот тип кривых полезен при построении связи напряжений с деформациями для данного материала. В дальнейшем-в ка­честве характеристики состояния при заданном уровне деформации стали использовать кривые зависимости напряжения от времени (также в лога­рифмических координатах). По ним для заданного уровня напряжения можно оп­ределить время, за которое достигается заданная деформация. Из этих кри­вых можно отобрать две наиболее полезные — зависимость минимальной скорости ползучести от напряжений (рис. 2.5) и зависимость времени до разрушения от заданного начального напряжения (рис. 2.6). Кривые первого