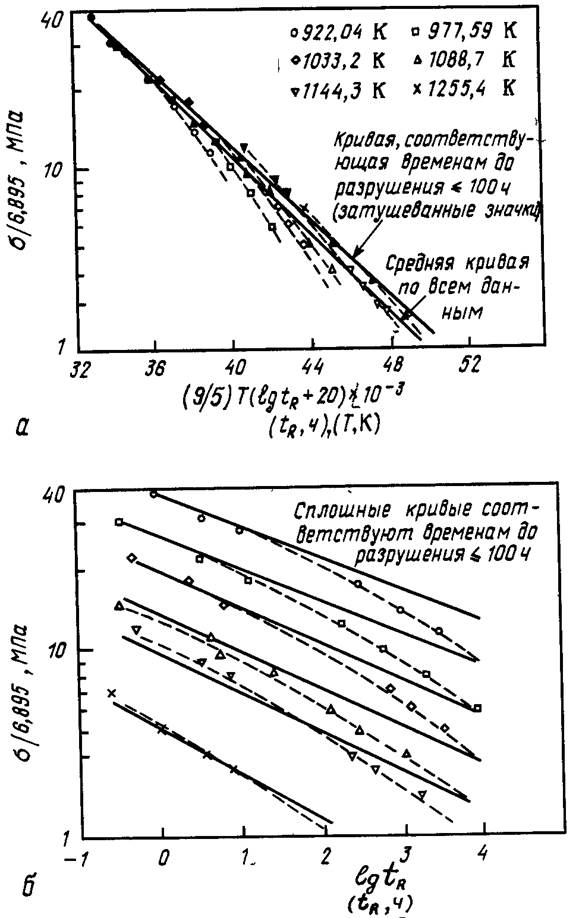
Рис. 11.9. Эталонные кривые разрушения нержавеющей стали (18%Сг — 8%). построенные с использованием параметра Ларсона — Миллера и графиков зависимости напряжения от времени до разрушения (см. работу [ 28]). Сплошные кривые при tR > 100 ч соответствуют аппроксимации зависимостей, полученных для «R< 100 ч,
идентифицировать. Систематизированный таким образом подход был назван "методом минимальной ответственности'1 ^, поскольку при этом подразумевается.что исследователь не должен брать на себя ответственность, с самого начала
*) Воригинале minimum-commitment method. — Прим, пврвв.
316
Глава ^Проектирование конструкций с учетом ползучести
ограничивая выбор одним параметром, а имеет возможность адаптироваться к любому параметру, какая бы форма его ни выявилась в процессе вычислений.
Разумеется, данный подход к решению проблемы экстраполяции основан на чисто феноменологических соображениях. В идеале, конечно, надо бы учитывать соответствующие физические механизмы разрушения. В ранних попытках для этого требовалось принимать субъективные решения в отношении численных значений некоторых материальных констант или же использовать экспериментальные данные высокого качества, а в результате не предполагалось никаких систематических способов экстраполяции. Отметим, что опубликованный недавно в работе [32] подход, развивающий это направление, основан на исследовании микроструктурных изменений, сопровождающих накопление повреждений.
Основная идея данного направления заключается в утверждении, что если преобразовать данные по разрушению при различных температурах по формуле
или же по формуле
где Т0 — характерная температура (например-, средняя температура исследуемого диапазона), а константы Н и / выбраны из условия минимума отклонения, то в результате должна получиться единая эталонная кривая. Как пример реализации этой идеи воспроизведем результаты Кокса и Эшби [ 32] для нержавеющей стали марки 304(рис. 11.10): гладкая кривая на рис. 11.10 получена с использованием теоретически найденных значений постоянных Н и / в предположении, что имеет место степенной закон ползучести и задан определенный механизм роста пор. Эту кривую можно использовать для экстраполяции.
11.2. 'ВЕРИФИКАЦИЯ И ОЦЕНКА ПРИГОДНОСТИ РЕЗУЛЬТАТОВ ТЕОРЕТИЧЕСКОГО АНАЛИЗА НАПРЯЖЕНИЙ
До этого момента мы изучали методики исследования напряжений, требования к данным по ползучести и моделирование поведения материала. Неизбежно возникает главный, решающий вопрос: насколько хорошо результаты теоретического. анализа напряжений в данной конструкции согласуются с результатами ее фактических испытаний на ползучесть9
В предыдущих главах книги было видно, что строгий анализ напряжений при наличии зависимости от истории нагружения конструкции в условиях ползучести может потребовать применения весьма сложных и трудоемких численных методов. Независимо от того, является ли использованный метод специализированным, пригодным только для исследования данной конструк-
11.2.Оценка результатов теоретического анализа напряжений
О,МПа 100
317
10
о 53В "С а 593 "С д 540 Т О 704 'С v 81B °С U 577 \С 0326 °С
10 10 2 ЮЗ
10s ts,4
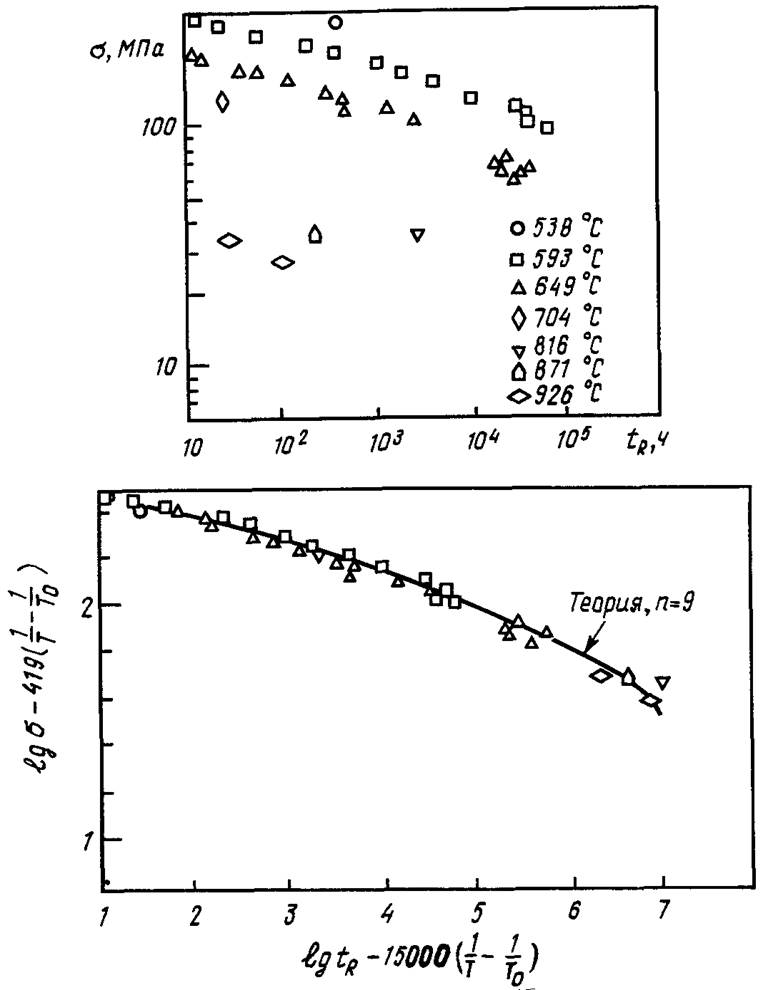
Рис, 11.10. Данные о разрушении при ползучести нержавеющей стали марки 304 в исходном (верхний рисунок) и нормализованном (с подобранными параметрами Н, J, Tjj) виде (см. работу [ 32], рис. 6).
Ции, или же речь идет о применении универсальных конечно-элементных комплексов программ, всегда существует проблема оценки достоверности и в конце концов принятия (или отбраковки) результатов анализа напряжений, поскольку проектирование должно основываться на этих результатах. Существуют два фактора, которые необходимо учитывать при оценке достоверности, - верификации и оценки пригодности. Верификация заключается просто в доказательстве, что анализ напряжений на самом деле, как и предполагалось, выполнен правильно, т.е. при формулировке задачи и ее решении не сделано грубых ошибок. Если это доказано (что при использовании универсаль-
71
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.