Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 20

Ф = аа₁ + Ьа + Зса_у,

Разрушение от макси­мальных напряжений

Смешанный тип разру­шений

Разрушение от эффектидного

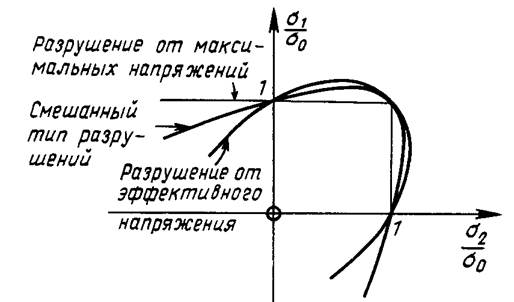
рис. 9,1. Изохронные поверхности разрушения.

9.2. Разрушение при сложном напряженном состоянии

253

Здесь а, Ь, с — экспериментально определяемые постоянные, причем

а + Ъ + с = 1.

Важность введенного понятия определяется тем, что, как замечено в опытах, напряженное состояние, вызывающее рост функции y(t) и, следова­тельно, увеличение поврежденности ю, совпадает с напряженным состояни­ем, соответствующим изохронной поверхности. Например, в коммерчески чистой меди, изохронная поверхность для которой соответствует максиму­му главных напряжений, поры и трещины наблюдаются преимущественно в плоскостях, перпендикулярных (растягивающему) главному напряжению. Та­ким образом, закон накопления повреждений можно записать в виде

u=Dll2ll.                                                             (9.3)

(1 -«)"*

Определяющие соотношения (9.2) и (9.3) основаны на результатах опытов на ползучесть при постоянных нагрузке и температуре. Поскольку поврежден-ность не является четко определенным физическим объектом, то в дейст­вительности ее трудно связать с уменьшением некоторой площади, и поэто­му поврежденность - это просто внутренний параметр состояния. Возмож­ность обобщения полученных уравнений на случай переменной нагрузки или переменной температуры является спорной. Кроме того, соотношения (9.2) и (9оЗ) можно критиковать и с некоторых других позиций, используя дополни­тельную экспериментальную информацию. Приведем здесь два принципиаль­ных замечания.

На рис. 9.1 изохронные поверхности разрушения для области сжатия не построены. Однако при исследовании конкретных конструкций может ока­заться, что существуют области сжимающих напряжений, для описания кото­рых нужны соответствующие определяющие соотношения. Вопрос о структу­ре таких соотношений является открытым. Можно, например, предположить, что уравнение (9.3) справедливо всюду, и тогда материал будет разрушаться при сжатии так же, как и при растяжении; можно принять также допущение об остановке процесса накопления повреждений при чистом сжатии, т.е. при оу< 0. Оба этих предположения являются спорными, поскольку для некото­рых металлов замечено, что при сжатии они проявляют способность к "самозалечиванию".

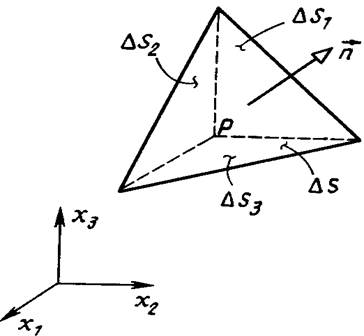
Во многих металлах поры и трещины возникают преимущественно по некоторым особым направлениям. Это означает, что совокупность количест­венных характеристик поврежденности должна содержать не только полный объем пор и скорость их распространения, но и эти особые направления. Ко­роче говоря, реальная поврежденность обладает анизотропией. Заметим, что эту анизотропию нельзя характеризовать только с использованием главных направлений тензора напряжений, о которых говорилось ранее. Данное за­мечание наводит на мысль о том, что использованная выше скалярная мера повреж­денности недостаточна - нужно ввести надлежащую тензорную характеристи­ку. К настоящему времени имеется немало формальных описаний накопления повреждений, однако попыток построить теорию накопления повреждений на основе тензорной меры не сделано¹). Одна из возможностей, кото­рые здесь возникают, состоит в обобщении рассмотренной выше концепции истинного напряжения на случай сложного напряженного состояния. Для того чтобы лучше увидеть, как это можно сделать, на время отвлечемся от основной темы и вернемся к тензорной форме записи, введенной в разд. 4=7.