Зафиксируем в теле произвольную декартову систему координат (xlt *2> *з ) и рассмотрим бесконечно малый тетраэдр, три плоские грани которого параллельны координатным плоскостям, а единичный вектор нормали к четвертой грани с площадью Д5 имеет компоненты П;. (рис. 9.2). Пусть pi— вектор плотности поверхностных усилий на грани Д5, тогда полное усилие, действующее на эту грань, равно &Spf = ст..Д5;-, где Д5. = Д5/г. -ориентированная элементарная площадь поверхности. Из выписанных соотношений следует хорошо известная формула Коши р,- = а . п • (см. разд. 4.7). Кроме того, их можно интерпретировать как обобщение обычного определения напряжения (а = Р/А 0 ) в опыте на чистое растяжение. В настоящей главе параметр со, характеризующий степень поврежденное™ материала, вводится с использованием истинной площади поперечного сечения (1 — а>)Ад, а определяющие соотношения записываются для истинного напряжения сг/(1 —со). Этот способ можно обобщить на случай сложного напряженного состояния, полагая, что компоненты вектора ориентированной площади Д5(. переходят в компоненты вектора истинной ориентированной площади Д S? , причем оператор перехода линейный, т.е.
Определяемый таким путем тензор второго ранга со., называется тензором поврежденности. Из формулы Коши вытекает, что полное усилие, неиз-
US.
Д5
Рис. 9,2. Бесконечно малый тетраэдр.
''Авторам, видимо , неизвестна работа А.А. Ильюшина "Об одной теории длительной прочности". — Механика твердого тела, 1967, № 3. — Прим, перев.
9.3. Пример: разрушение при ползучести многостержневой системы
255
менное в процессе разрушения и действующее на истинную площадку, равно ст.*. as? , где o*j— тензор истинных напряжений. Поскольку
*, . AS , = ctk ( 5kj - »fc/ )-'Д5; = а*. Д Sf ,
то, следовательно, компоненты тензора истинных напряжений определяют-
ся выражением
Тензор о%* , вообще говоря, несимметричен, и вместо него удобнее использовать следующий симметричный тензор истинных напряжений:
где Ф.. = (Б.. - со;-)"1 - тензор эффективных повреждений. Следует отметить, что теперь мы имеем трехмерный вариант феноменологической концепции истинного напряжения. Критерием разрушения при ползучести в этой теории, обобщающим скалярный критерий со= 1, является требование, чтобы тензор 8у - со^. , рассматриваемый как матрица, был необратимым (т.е. вы-
рожденным).
Нужно сказать, что проблема построения определяющих соотношений для третьей стадии ползучести пока находится в зачаточном состоянии. Нетрудно видеть, в частности, что определяющие соотношения, основанные на использовании тензорной меры поврежденности, чрезвычайно сложно применить для решения практических задач. Именно поэтому будет использовано лишь простейшее уравнение (9.3), которого достаточно для описания изотермической ползучести конструкций при постоянном (или пропорциональном) нагружении. Это позволит решить некоторые частные задачи анализа напряжений при наличии повреждений, а также проиллюстрироватьприменение соответствующих чис-
ленных методов.
Приведем полностью используемые нами далее уравнения, записанные в главных осях для полной деформации е = е£ + ес , где для упрощения принимаем
*,
(!-«)*
(9.4)
(1 - со)"
Будем предполагать, что материальные константы связаны частным соотношением k = 0,7. Эти соотношения являются идеализацией, которая тем не менее прекрасно подходит к рассматриваемым нами задачам.
9.3. ПРИМЕР: РАЗРУШЕНИЕ ПРИ ПОЛЗУЧЕСТИ МНОГОСТЕРЖНЕВОЙ СИСТЕМЫ
Краткое исследование напряжений при наличии повреждений в матери-алеЧЬчнем с простой задачи, для которой нужны только одномерные определяющие уравнения. Кроме того, на примере этой задачи будут выявлены не-
9.4. Теория разрушения сплошной среды
261
7 0,5
0,1
L, 1,1
0,1 7 10 10* Ю3
Г/?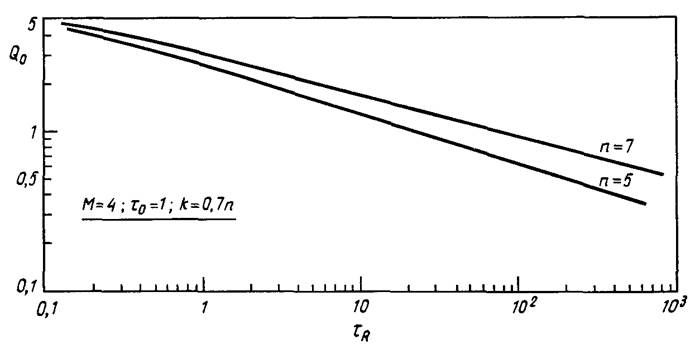
Рис. 9.6. Связь приведенного времени до разрушения с нормализованной внешней нагрузкой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.