скорость увеличения поврежденности неограниченно растет (со —»+ <«), По определению мгновенное повреждение при нагружении определяется параметром сор = £$)<% , следовательно, нагрузка, которая приводит к мгновенному хрупкому разрушению, может быть найдена из уравнения
Изложенная здесь теория не очень полезна для моделирования поведения более сложных крнструкций, поскольку она предсказывает скачкообразный переход от вязкого разрушения к хрупкому, что конечно, в действительности ' не реализуется, а скорее всего существует плавный переход от одного типа разрушения к другому. Кроме того, при исследовании конкретных конструкций заранее неясно, какой механизм разрушения является доминирующим. Можно бцло бы, разумеется, сконструировать теорию с гладким переходом от одного типа разрушения к другому путем, например, комбинации моделей хрупкого и вязкого разрушения. Однако здесь мы не будем стремиться к этому, поскольку в случае, когда деформации малы, механизмом вязкого разрушения скорее всего можно пренебречь и сосредоточить внимание на изучении хрупкого разрушения. Этот подход привел к созданию нового раздела механики разрушения, получившего название континуальной механики разрушения, которая представляет собой инструмент для описания разрушения вследствие накопления повреждений нагруженных конструкций. Один из путей построения математической модели данного явления состоит в том, чтобы ввести в качестве параметра состояния параметр поврежденнос-ти в уравнения состояния, приведенные в предыдущем разделе, например
«c=f(a,co), co=g(<j,co). (2.8)
Здесь параметру со не олудует обязательно придавать определенный физический смысл. Текущее напряжение с и начальное напряжение aQ отождествляются, так что, например, уравнения (2.8) можно привести к виду
(2.9)
Эти определяющие уравнения можно использовать вместо уравнения (2.1), в частности, когда существенной является третья стадия ползучести. Предполагается, что эти уравнения верны для переменной нагрузки, однако их можно усовершенствовать и уточнить, вводя другие дополнительные параметры состояния. Сейчас мы оставим на время проблему разрушения при ползучести, однако в последующих главах мы к ней вернемся.
ГЛАВА 3
ПОВЕДЕНИЕ ПРОСТЕЙШИХ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
При исследовании сложных конструкций необходимо произвести обобщение одномерных определяющих уравнений, выведенных в предыдущей главе, на случай сложного напряженного состояния. Однако некоторые простейшие элементы - балки, стержневые конструкции — можно изучить, используя одномерные уравнения. В этой главе будут исследованы некоторые из этих конструкций с тем, чтобы подойти к основным методам анализа напряжений при ползучести, а также для иллюстрации возможных здесь простых аппроксимаций, которые будут в дальнейшем использованы. Всюду ниже будут рассмотрены простейшее определяющее уравнение скоростного типа для переменных напряжений и степенной закон ползучести, а именно I = &/E + g(t)o". Начнем наше исследование с классической задачи - задачи об установившейся ползучести балки при изгибе. При установившейся ползучести напряжения и скорости деформаций в конструкции постоянны во времени, так что материал испытывает вторую стадию ползучести и, следовательно, определяющее уравнение приобретает простейший вид i = В а".
3.1 ПРИМЕР: УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ БАЛКИ ПРИ ИЗГИБЕ
Рассмотрим балку, поперечное сечение которой с площадью А обладает двумя плоскостями симметрии (рис. 3.1). Будем предполагать, что имеет место чистый изгиб, когда плоские до деформации поперечные сечения остаются плоскими после деформации — существенны лишь продольная (осевая) деформация е и продольное напряжение о-. Условие совместности деформации и кривизны kобеспечено, если
-Ау.
(3.1)
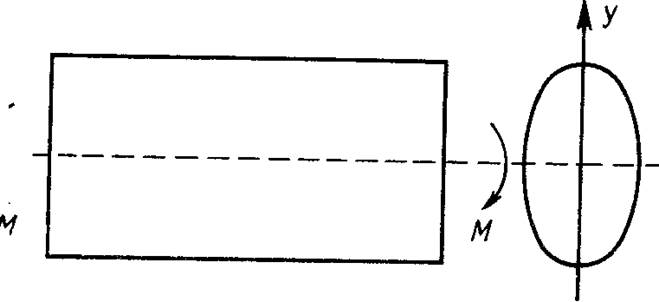
Рис. 3./. Геометрия изгибаемой балки.
М
204
Глава 7. Анализ напряжений при неустановившейся ползучести
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.