Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 8

2.2  ФИЗИЧЕСКИЕ МЕХАНИЗМЫ ПОЛЗУЧЕСТИ

Следующий этап состоит в том, чтобы на основе описанных выше экспе­риментальных данных построить математическую модель поведения мате­риала и далее использовать ее для анализа напряжений. В настоящей работе моделирование явления ползучести будет проведено с использованием фено­менологического подхода. Это означает, что поведение материала характе­ризуется на базе наблюдений на макроуровне, а не на ,лежащих в основе ис­следуемого явления физических процессах. Такой подход - обычный при ис­следовании напряжений и в материаловедении. Однако к настоящему време­ни достигнуто и достаточно глубокое понимание физических механизмов ползучести - об этом будет кратко рассказано ниже.

Существуют два основных механизма - так называемые дислокацион­ная ползучесть и диффузионная ползучесть. Дефекты кристаллической ре­шетки металла, известные как дислокации, движутся сквозь решетку, прео­долевая естественную прочность решетки, а также сопротивление различ­ных содержащихся в ней примесей, препятствующих ползучести. При неболь­ших напряжениях движение дислокаций прекращается или замедляется, од­нако ползучесть продолжается из-за движения большого количества атомов — диффузионного течения из зоны сжатия в зону растяжения. Дислокацион­ная ползучесть обнаруживает сильно нелинейную зависимость от напряже­ний, о которой щла речь в предыдущем разделе. При диффузионной ползу­чести реализуется примерно линейная зависимость вязкого типа от напряже­ний. Следует подчеркнуть, что наиболее важным механизмом ползучести для большинства инженерных конструкций является дислокационная ползу­честь.

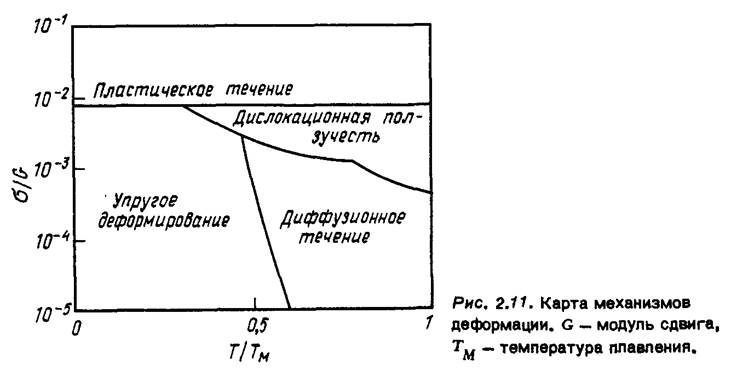
Преобладающую роль того или иного механизма в различных диапазонах изменения напряжений и температуры можно показать на обобщенной диа­грамме механизмов деформации (рис. 2.11). Это идеализированная схема для частного материала, на которой существуют как зоны мгновенных плас­тических деформаций, так и зоны, в которых деформации чисто упругие. Лег­ко видеть, что деформации ползучести становятся заметными при темпера­туре, примерно равной 0,3 Т_и, где Т_м - температура плавления материала.

26

Глава 2.Феноменологическое описание ползучести

10

-2

10-"

10

-5

_ Пластическое течение

^Дислокационная пол­зучесть

' Упругое

деформирование    \ Диффузионное течение

0,5

Рис. 2.11. Карта механизмов

1   деформации. G - модуль сдвига, t_u— температура плавления.

2.3  ПРОСТЕЙШИЕ ОДНОМЕРНЫЕ ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ

Для описания стандартных кривых ползучести предложено много упро­шенных одномерных определяющих уравнений. Мы сосредоточим наше вни­мание на временах, отвечающих первой и второй стадиям ползучести, игно­рируя третью стадию, и приведем несколько соотношений, нашедших наи­большее применение в анализе напряжений.

Первым шагом почти во всех подходах является разделение деформа­ций на упругую и пластическую составляющие:

6"^е£ + «С

- это соотношение можно считать определением деформации ползучести. В общем случае деформация ползучести является функцией напряжения а , времени J и температуры Т: е_с -/(a,t, Т), которую обычно предполагают имеющей вид произведения

Приведем предложенные различными авторами функциональные зависи­мости от напряжений:

/i(o- ) - Во" /,(сг) - Csh(aa ) /I (a ) * Оехрфо-) f,(a)- AtsMyo-)]" /_t (о- ) - В(ст - 6* )"

-  закон Нортона,

-  закон Прандтля, — закон Дорна,

-  закон Гарофало,

-  закон трения,

2.3. Простейшие одномерные определяющие уравнения

27

в которых все символы, не совпадающие с о-, обозначают материальные константы.

Отметим, что соотношение Гарофало содержит как частные случаи законы Нортона, Прандтля и Дорна и предсказывает "криволинейность" зависимости минимальной скорости ползучести от напряжений (рис. 2.5). Кроме того, степенной закон Нортона вытекает также из физических сооб­ражений и очень широко используется на практике.

В качестве временных зависимостей были предложены следующие соотношения:

f_t(t)»t                           - для второй стадии ползучести,