Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 12

2.4. Разрушение при ползучести

33

Рис. 2.13. Цилиндрический стержень при постоян­ной нагрузке.

£-0

>Р t>0

по предположению, ползучесть происходит при постоянном объеме, то А₀1₀=:А1, Напряжение вычисляется по формуле и = Р/А. Если мы пренебре­жем упругими деформациями и рассмотрим вторую стадию ползучести, описы­ваемую степенным законом, то, объединяя полученные выше результаты, найдем, что

_£.

A

и, следовательно, A» -¹dA= - Ba£ Интегрируя, получим nBa£ t = 1 - (A/A₀)ⁿ.

Как видно из этого выражения, величина А уменьшается до нуля за конечное время - время до разрушения

1

nBa"

(2.6)

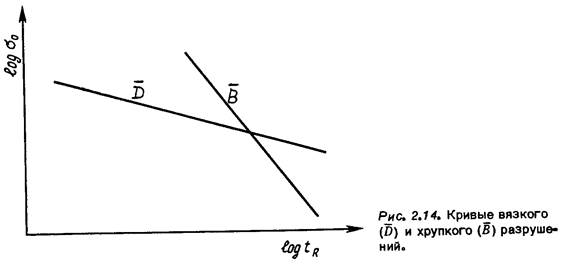
Полученная зависимость времени до разрушения от начального напряжения в логарифмических координатах изображается прямой линией (рис. 2.14). Данная теория вязкого разрушения на практике дает не очень хорошие ре­зультаты, поскольку было пренебрежено упругой деформацией и первой ста­дией ползучести. Несмотря на то что теория должна быть достаточно точной в случае, когда вторая стадия ползучести преобладает, формула (2.6), вооб­ще говоря, дает завышенную оценку времени до разрушения. Кроме того, из Нее следует, что любая конечная нагрузка приводит к конечному времени До разрушения. В действительности же экспериментально установлено, что существует нагрузка, при которой образец разрушается мгновенно. Так

34

Глава 2.Феноменологическое описание ползучести

как предполагается, что деформации конечны, должна иметь место также мгновенная пластическая деформация. Используя для иллюстрации теорию полных деформаций, имеем е = е_р + е _с, ер = В₀а"°. Упругая деформация при этом по-прежнему не учитывается.

Используя выражение для логарифмической меры деформации и усло­вие несжимаемости, получим

„  "о/ 4ЛМ   _./V

-"oVo   (-г)    Г ^F

\  Л   IJ

Разрушение наступает при А -»°о и конечном значении площади поперечно­го сечения, -равном A_R=(„₀ g^) ^Vno_PaНагрузка р_о, при которой происходит мгновенное разрушение, соответствует равенству A_R = А₀, следовательно,

P₀=V(n₀B₀)^V"<>.

В теории хрупкого разрушения изменением геометрии образца прене­брегают. Предполагается,   что при ползучести в объеме образца возникают поры, увеличивающиеся с течением времени, которые уменьшают эффек­тивное поперечное сечение, воспринимающее нагрузку. Для описания это­го явления вводится параметр поврежденности со таким образом, что эф­фективное поперечное сечение равно величине (1 — <о)Л₀₁ а истинные напря­жения определяются формулой

*-±         ^Р

А         А₀(\ - «)

Параметр со возрастает от 0 до 1 при переходе образца из исходного состоя­ния в состояние разрушения. Параметр поврежденности - пример скрытого (внутреннего) параметра, введенного в предыдущем разделе, для которого мы должны установить надлежащее кинетическое уравнение. Будем предпо­лагать скорость возникновения повреждений зависящей от текущего значения истинного напряжения, так что со= Ост*. Это соотношение можно преоб­разовать, исключив из него напряжение, чтобы найти время до разрушения

dco

1

(2.7)

Получившаяся зависимость в логарифмических координатах также представ­ляет собой прямую линию (рис. 2.14). Анализируя графики на рис. 2.14, ви­дим, что k < п и D > В, Условием разрушения в предложенной модели хруп­кого разрушения является равенство со» 1, что соответствует уменьшению площади поперечного сечения до нуля. Однако, как и в случае вязкого раз­рушения, хрупкое разрушение может наступить при конечном значении пло­щади поперечного сечения, откуда аледует, что параметр сов момент разру­шения меньше 1 . Одним из способов учета этого обстоятельства в нашей модели будет предположение, что в начальный момент времени имеет место мгновенное повреждение, так что прлное повреждение представляет собой сумму мгновенного и накопленного повреждений. Как и выше, для иллюстра­ции предположим, что мгновенная часть степенным образом зависит от ис­тинного напряжения; следовательно,

__₀ at

Отсюда имеем

и, ес.ли выпрлнено условие

)]"<"о^т".1.