Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 30

В первом примере будем предполагать, что полная деформация ползу­чести представима в виде суммы деформаций первого и второго этапов f 14]

Здесь

), e= Во-".

Этот тип модели с применением полных деформаций часто используется в методе конечных элементов ; здесь необходимо найти шесть материальных констант: К, m, a, Ь, В к п. Константы определяются по стандартным кри­вым ползучести следующим образом (рис. 11.2).

а . По данным об установившейся ползучести вычисляем константы В я п.

Ь . Формируем составляющую деформации первой фазы ползучести

Находим предел, к которому стремится эта деформация с ростом времени. Установлено, что зависимость данного предела s °° от напряжений в логарифмических координатах примерно линейная; следовательно, можно найти константы К и т , для которых

Ер⁰   =   Кс^т.

с. Формируем величину (1 - е /6°^). Установлено, что эта величина с увеличением времени экспоненциально убывает и в значительных пределах не зависит от напряжения. Следовательно, можно найти оставшиеся две константы а и  Ь, для которых а* = ]-_вр/е-=«е-*',

используя, например, метод наименьших квадратов для обработки всей совокупности данных.

В качестве второго примера рассмотрим модель Бейли — Орована (разд. 2.3), в которой требуется определить четыре материальные константы- k_t, k₂, т и п. Эти константы определяются следующим образом [15].

11.1.Моделирование поведения материала при проектировании

307

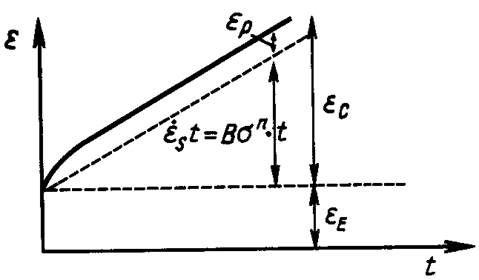
Рис, 11.2. Косвенная идентификация модели ползучести, использующей полную деформацию.

-at

а.  По данным об установившейся ползучести вычисляем В = k_ltk₂и п.

б.  Проводим ряд опытов на обратную ползучесть, в которых напряже­ние на стадии установившейся ползучести уменьшается на величи­ну Асг. Если разгрузка происходит в точке А (рис. 11.3), то будет

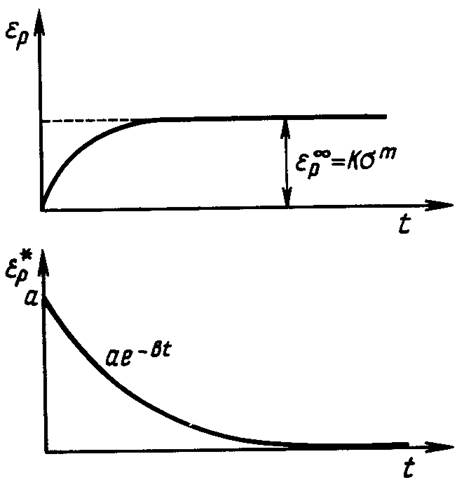
Рис. 11.3. Косвенная идентификация моде­ли ползучести Бейли — Орована.

308

Глава 11.Проектарование конструкций с учетом ползучести

существовать период Д t, на протяжении которого скорость дефор­мации ползучести равна нулю, после чего, начиная с точки В, на­ступает этап роста деформации, продолжающийся до установления, причем скорость вновь установившейся ползучести будет меньше той, которая была перед разгрузкой. В течение данного промежут­ка текущее напряжение Rуменьшается от а до о- — Да, причем

dR/dt= -r(R) = k_l| R\ⁿ~^m.

Функцию г можно определить, переходя к пределу при Да -+0; при этом начальный уровень напряжений для нее будет равен а, | а | = R. В логарифмических координатах данная функция будет примерно линейной; следовательно, константы k_lи (п - т) можно найти методом наименьших квадратов.

Очевидно, что метод прямой идентификации содержит несколько простых и ясных процедур, при реализации которых от исследователя не требуется ни­каких субъективных решений. Однако, как уже отмечалось, этот метод непри­меним в случае теорий с внутренними параметрами состояния. В то же время метод косвенной идентификации учитывает историю процессов деформирова­ния и является более предпочтительным. Недостатком метода косвенной иден­тификации является отсутствие оценок возможных вариаций параметров; эти оценки можно найти, используя стандартные формулы метода прямей иденти­фикации.

11.1.3. Корреляция и экстраполяция данных