Методы ана­лиза напряжений в конструкциях с учетом деформаций ползучести, страница 25

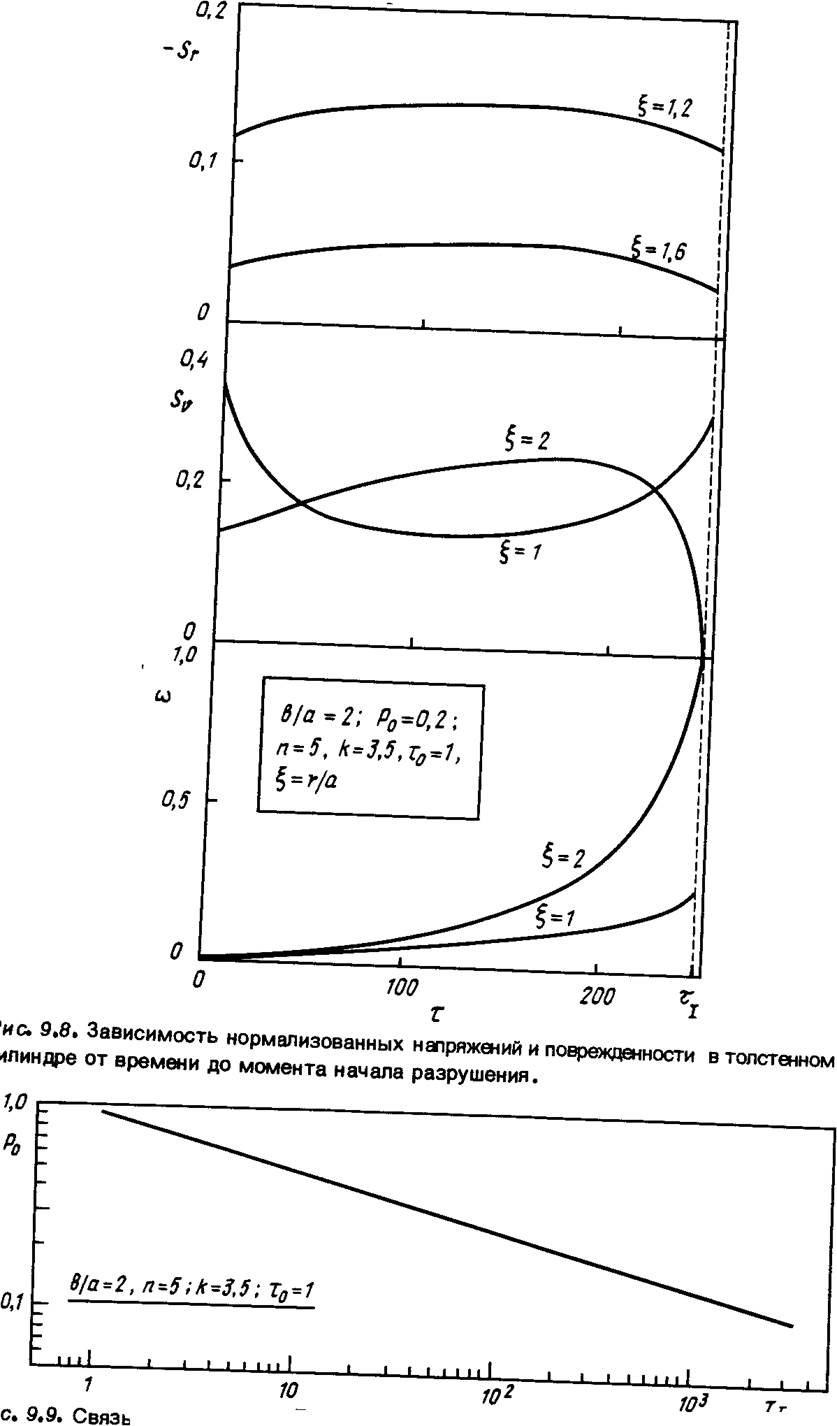
Вначале построим численное решение рассматриваемой задачи на стадии скрытого разрушения для одного частного значения показателя п, принимая k = 0,7л, и для различных значений параметра нагрузки р₀. Типичные про­цессы перераспределения напряжений s_qи  s_r  и зависимость параметра поврежденности со от времени до момента tj (начала разрушения) приве­дены на рис. 9.8. Видно, что в рассматриваемом случае разрушение начи­нается на внешней границе цилиндра, и, следовательно, можно ожидать, что в дальнейшем оно будет распространяться внутрь. При подходе к моменту разрушения напряжение на внешней поверхности быстро спадает до нуля. На рис. 9.9 показана зависимость времени до начала разрушения от нагрузки. Отметим, что для исследуемого здесь типа нагрузки разрушение начинает­ся всегда на внешней поверхности цилиндра (хотя в общем случае это не так — в зависимости от используемого уравнения для накопления повреждений раз­рушение может начинаться на внутренней поверхности и даже в некоторой внутренней точке стенки цилиндра). Постановку задачи теперь следует сфор­мулировать заново, с тем чтобы учесть эффект распространения фронта разрушения.

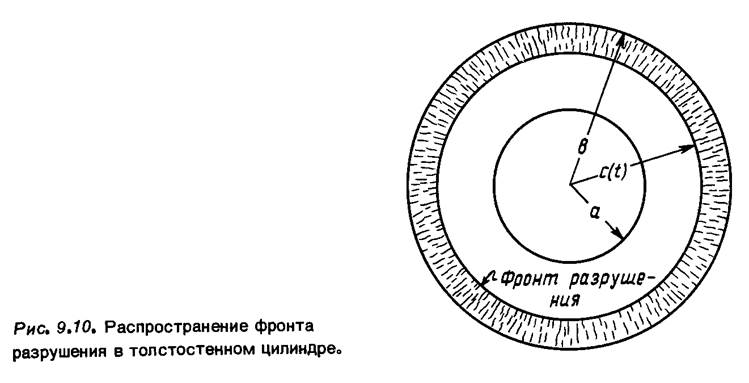
Пусть радиус фронта разрушения равен с (г) (рис. 9.10), тогда в облас­ти с< г< Ь материал разрушен. Уравнения (9.9) и (9.11) в неразрушенной зоне a< г < с по-прежнему применимы, однако уравнение (9.10) необходи­мо изменить. В случае неподвижного фронта разрушения имеем

^

*

(9.12)

В области а ^ г ^ с эквивалентные упругие напряжения равны

а операторы задачи об остаточных напряжениях определяются формулами

дг.    Е       (^г_{ ^r2(l-v²)U

_f^c    f ^Er ~^ee

г²-а²     с^{2      с}_г

2(1 - v²)      г²

 

^{ПрИВадвННОГ}°

«о "ачапа разрушения с нормализованным

9.5. Разрушение при ползучести толстостенной трубы

269

2(1-V²)        гПа

Ev

1-v²

+ vs^);

C\.

с   _e?-e.^C

£v(l-2v] 1-v²

c²-a²₀

nif-

Г—

- w²

которые для ясности приведены полностью.

Уравнения (9.9), (9.11) и (9.12) можно преобразовать к дискретной фор­ме, для чего используется следующая вычислительная процедура. В момент начала разрушения, которое наступает в крайних точках, где радиус равен ^гц, деформацию ползучести в этих крайних точках из вычислительного про­цесса можно исключить, после чего ставится новая задача для оставшихся точек г; , i = 1,2,..., М -1, до которых фронт разрушения пока не дошел. Вновь используется алгоритм решения, который продолжает действовать До того момента, пока фронт разрушения не подходит к точке г_м _ _х; после исключения этой точки производится новая переформулировка задачи с ана­логичным алгоритмом, процедура повторяется до тех пор, пока критерий разрушения не будет выполнен для всех точек. Таким путем можно просле­дить распространение фронта разрушения; из способа построения числен­ного решения видно, что фронт разрушения движется скачкообразно.

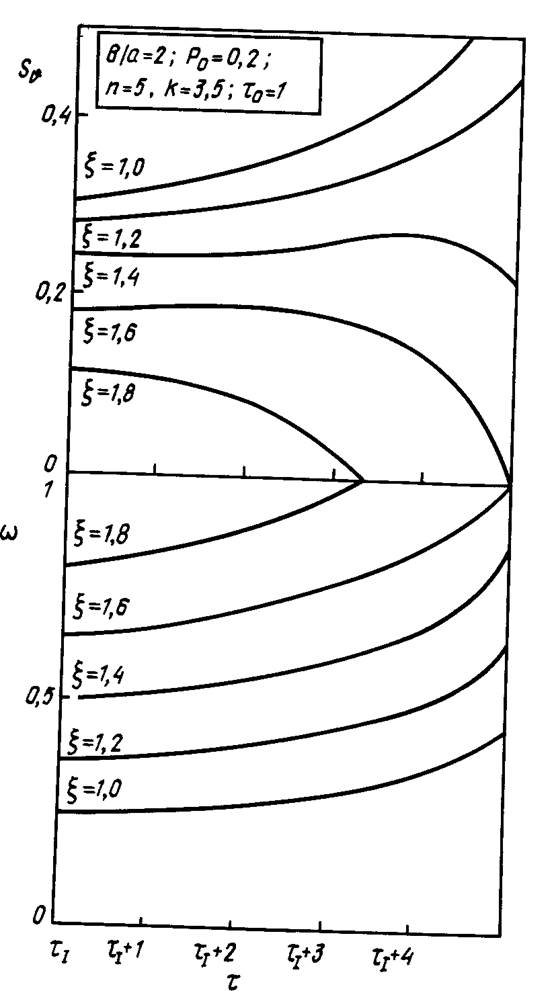
На рис. 9.11 показаны процессы перераспределения напряжения s_qи накопления повреждений со на стадии распространения разрушения. Очевид­но, что движение фронта разрушения соответствует движению точки, в ко-

270

Глава 9. Разрушение при ползучести

Рис. 9.11. Изменение нормализованного окружного напряжения и поврежденное™ в процессе распространения разрушения.

торой напряжения падают до нуля. На рис. 9.12 приведена типичная зависи­мость безразмерного радиуса фронта разрушения c(t)Jaот времени. Вид­но, что по мере продвижения фронта разрушения в глубь цилиндра скорость его движения возрастает. И наконец, на рис. 9.13 приведен график зависи­мости отношения (tjj - tj )/tj , характеризующего продолжительность стадии распространения разрушения, от параметра нагрузки р₀.

, 9.5. Разрушение при ползучести толстостенной трубы

2\

271

в/а=2; Р_а=0,2; /7=5; k=3,5,

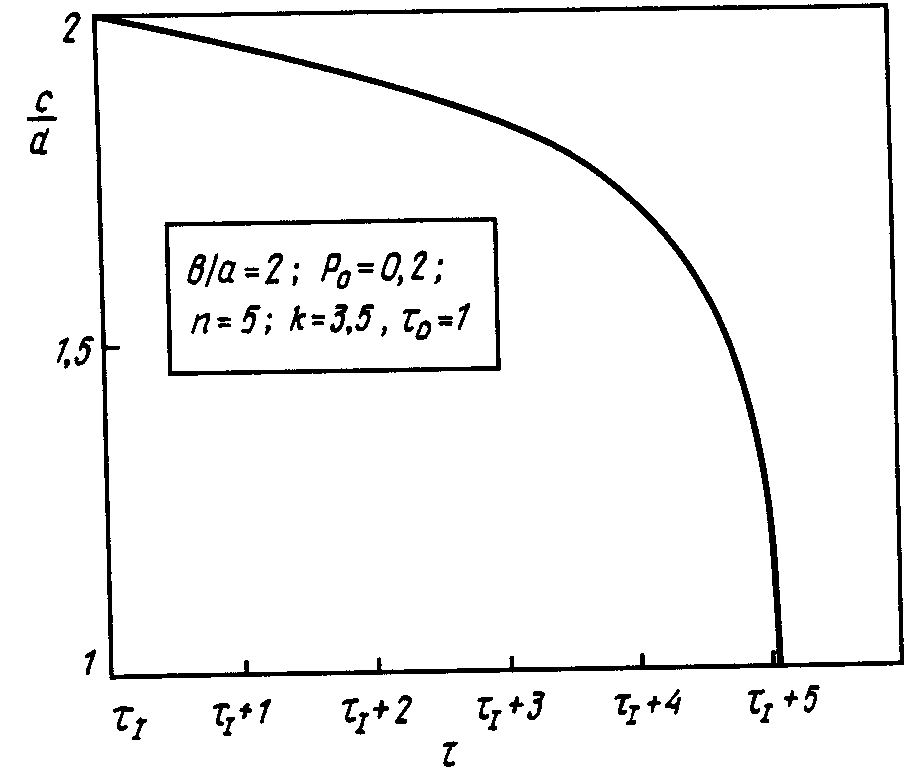
Рис.  9.12. Зависимость радиуса фронта разрушения от времени.

О                                   0,5                                7

Ра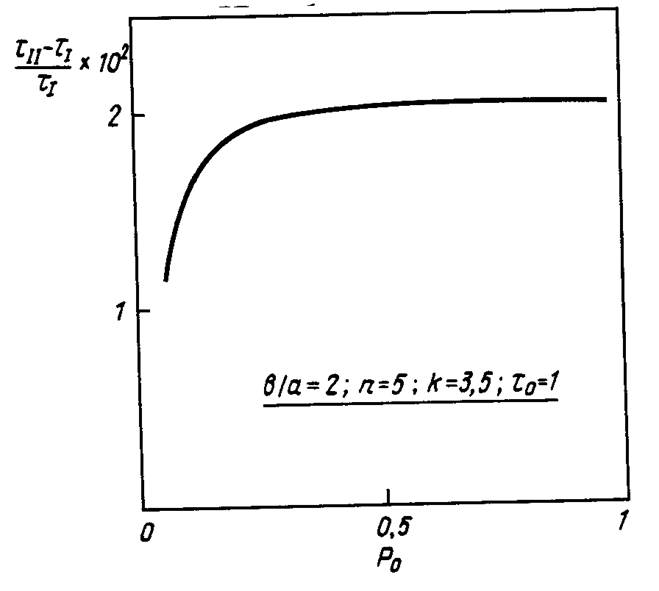

Рис. 9.13. Зависимость отношения длительности фазы распространения разрушения ко времени до момента начала разрушения от приложенного давления.

ГЛАВА 11