- общее среднее по результативному
признаку и nj – численности совокупностей выделенных групп
по факторному признаку.
Внутригрупповая дисперсия рассчитывается по каждой из выделенных групп,
выделяемых по факторному признаку, а затем из этих внутригрупповых дисперсий
рассчитывается средняя внутригрупповая 
.
Внутригрупповая дисперсия учитывает вариацию результативного признака, обусловленную вариацией прочих (неучтенных) факторов, кроме факторного признака.
Внутригрупповая дисперсия результативного признака по каждому из выделенных групп рассчитывается по формуле:
а) по несгруппированным данным
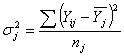
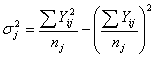
б) по сгруппированным данным
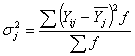
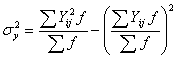
По вариационным рядам с равными интервалами целесообразно применять способ условных моментов:
Средняя внутригрупповая дисперсия:
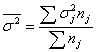
Отношение межгрупповой дисперсии к общей наз-ся коэф-том детерминации (причинности):
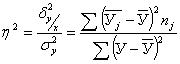
Коэф-т детерминации обозначает удельный вес вариации результативного признака, обусловленную вариацией факторного признака.
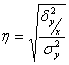- коэф-т корреляционного отношения.
Он показывает тесноту связи между результативным и факторным признаком.
И коэфф-т корреляционного отношения 
и коэфф-т детерминации
варьируются от 0 до 1.
Если 
и 
= 1,
то связь между результативным и факторными признаками полная (функциональная).
Рассмотренное правило сложения дисперсий выполняется при условии расчета дисперсий по генеральной совокупности.
Применительно к выборке оценка дисперсии дается на одну степень свободы.
16. Стат. хар-тики асимметрии и эксцесса.
Применительно к массовым соц-экон. явлениям действует закон нормального распределения:
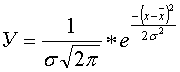
Графически нормальный з-н распределения выглядит так (колокол Гауса):
При строго симметричном распределении значение средней, моды, медианы совпадают6
Под воздействием как случайных, так и существенных причин строго симметричное распределение может стать асимметричным.
Различают асимметрию левостороннюю (отрицательную) и правостороннюю (положительную).
При положительной асимметрии имеем 
, а
при отрицательной - 
.
Наиболее простой мерой ранжирования (расположения) асимметрии явл-ся разность между медианой или модой.
Для сравнения степени асимметрии в двух или нескольких рядах с различными единицами измерения исп-ся след. пок-ли асимметрии (As).
а) 
б) 
Наиболее широко в кач-ве пок-ля оценки асимметрии выступает соотношения третьего центр. vомента к среднему квадратического отклонению в кубе, т.е.
Основание для исчисления пок-ля асимметрии по данной формуле служит мат. доказанное положение о том, что все нечетные центральные моменты равны 0.
Вследствие этого неравенство нулю третьего центрального момента исследуемого ряда распределения указывает на его асимметричность.
Асимметрия может быть: значимой (существенной) и незначимой.
Для измерения значимости (незначимости) асимметрии исп-ся специальный t-критерий исчисляемый по формуле:
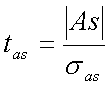, если tas>3, асимметрия в ряду распределения
признается значимой (существенной) и наоборот.
Среднеквадратическая (стандартная) ошибка коэфф-та асимметрии исчисляется по формуле:
,
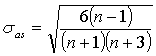n – число наблюдений
Применительно к интервальным рядам распределения с равными интервалами значения центральных моментов можно выразить через сис-му условных моментов. В этом случае условные моменты рассчитываются по кратным значениям интервала:
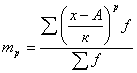
При расчете центральных моментов поправки на кратное значение К производить не будем.
В этой сис-ме расчетов 
Третий центральный момент на основе комбинации условных моментов вычислим из:
Для хар-тики степени отклонения симметричного распределения от нормального рассчитывается пок-тель островершинности (показатель эксцесса) Ex, исчисляемый по формуле:
Для кривой нормального распределения Ex=0.
Эксцесс может быть положительным и отрицательным.
У высоковершинных пок-ль эксцесса – положительный, а у плосковершинных отрицательный.
Ex – число отличенное (без ед. измерения).
Предельное значение отриц. эксцесса равно 2, а островершинного – величина бесконечная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.