Значение четвертого центрального момента при помощи сис-мы условных моментов вычислим по след. выражению:
![]()
Вывод о том, присущ ли эксцесс генер. сов-сти судят по t-критерию эксцесса:
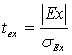 ,
,
Если tex>3, то эксцесс свойствен генер. сов-сти и наоборот.
Основная (среднеквадратическая) ошибка эксцесса рассчитывается по формуле:
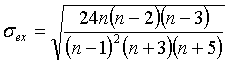
Рассм. правило сложения дисперсий применительно к дисперсии альтернативного признака.
Общая дисперсия альтернативного признака исчисляется по формуле:
![]() ;
; ![]()
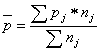 , или
, или 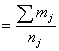 .
.
Межгрупповая дисперсия альтернативного признака рассчит-ся по формуле:
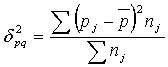
Внутригрупповая дисперсия по каждой из выделенных групп расчит-ся по формуле:
![]()
Средняя внутригрупповая дисперсия долей опред-ся по формуле:

Таким образом, ![]()
17. Способы разложения общей дисперсии альтернативного признака
Альтернативным наз-ся признак, принимающий два взаимоисключающих значения: или события, или нет. Для единиц совоупности наступления признака обозначается единицей, а ненаступление – «0». В долях (удельный вес) наступление событий обозначается «р»; не наступление «q».
Р=m/n; q=(n-m)/n=1-р; р+q=1
Вычислим среднее значение альтернативного признака:
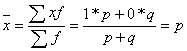
Вычислим дисперсию альт. признака:
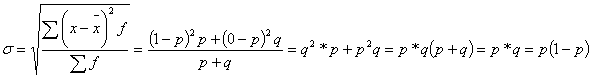
Т.о. дисперсия альт. признака равна произведению долей противоположных событий.
Рассм. правило сложения дисперсий применительно к дисперсии альтернативного признака.
Общая дисперсия альтернативного признака исчисляется по формуле:
![]() ;
; ![]()
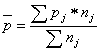 , или
, или 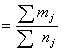 .
.
Межгрупповая дисперсия альтернативного признака рассчит-ся по формуле:
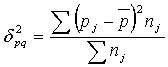
Внутригрупповая дисперсия по каждой из выделенных групп расчит-ся по формуле:
![]()
Средняя внутригрупповая дисперсия долей опред-ся по формуле:

Таким образом, ![]()
18. Методология стат. изучения закон-стей распределения. Выравнивание частот по з-ну нормального распределения.
Для получения приблизительного представления о форме распределения строят соответствующие графики. Число наблюдений, по к-рому строится эмпирич. распределение, обычно невелико и представляет собой выборку из исследуемой ген. сов-сти. В связи с этим эмпирич. данные в определенной степени связаны с влиянием случайных причин, величина к-рых неизвестна. Влияние этих случайностей искажает основную закономерность изменения величин признака.
С увеличением числа наблюдений и одновременным увеличением величины интервала зигзаги начинают сглаживаться и впределе мы приходим к плавной кривой, к-прая наз-ся кривой распределения.
Кривая распределения характеризует теоритическое распределение, т.е. то распределение, к-рое получилось бы при полном погашении (выравнивании) случайных причин, искажающих (сглаживающих, затемняющих) основную закономерность.
Исследование закономерности или формы распределения включают в себя решение трех последовательных задач:
1.выяснение общего характера распределения (нормального, биноминального, логистического и др.). 2. выравнивание (сглаживание) эмпирического распределения, к-рое состоит в том, что на основании эмпирического распределения строится теоритическая ф-ция распределения, т.е. У=f(х) с заданной формой. 3. проверку соответствия теорит. распределения эмпирическому. В практике стат. исследования приходится встречаться с самыми различными распределениями.
При изучении однородных совокупностей имеем дело, как правило, с одновершинными распределениями.
Многовершинность свидетельствует о неоднородности изучаемой сов-сти. наличие двух и более вершин в ряде распределения говорит о том, что необходима группировка данных.
Выяснение общего х-ра распределения предполагает оценку степени его однородности. Симметричным явл-ся такое распределение, в к –ром частоты любых двух любых вариантов равностоящих в обе стороны от центра равны между собой (т.е. их х(средняя)=Ме=Мо). Оценка существенности пок-лей асимметрии и эксцесса позволяют сделать вывод о том, можно ли отнести данное эмпирич. распределение к типу кривой нормального распределения.
Распределение непрерывной случайной величины применительно к з-ну норм. распределения имеет вид (ГРАФИК)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.