В научных исследованиях рекомендуется формула Стерджесса определения величины равного интервала: i = (Xmax -Xmin)/(1+3,322lgN). Обычно эта формула используется при достаточно большом объеме изучаемых статистических совокупностей. Число групп подбирается эмпирически, с таким расчетом, чтобы интересующая нас закономерность проявилась достаточно четко и при этом в каждой группе должно быть достаточно большое число наблюдений. В статистической практике даже при достаточно большой вариации группировочного признака не рекомендуется выделять более 12 групп, даже если большие вариации.
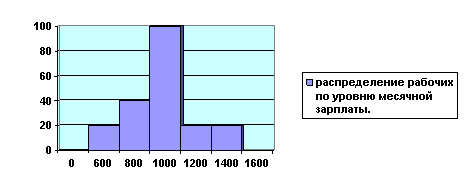Графическое изображение интервальных рядов
распределения осуществляется в виде гистограммы:
Гистограмму можно представить и в виде полигона частот. Для этого необходимо взять середину интервалов, а затем соединить кривой эти точки.
Если ряд распределений построен по неравным интервалам, то в этом случае гистограмма строится по плоскости распределения частот на единицу интервала.
Кратные интервалы – используются со знаменателем геометрической прогрессии равным 2. Такой подход позволяет показать относительные различия между группами. Целесообразность такого подхода связана с тем, что вариация группировочного признака весьма значительная и по величине равных интервалов такой ряд распределения построить невозможно.
σ2=(∑(x-xср)2ƒ/ ∑ƒ)½.
В интервальных рядах распределения, построенных по непрерывным признакам, положение интервалов интерпретируется так: верхняя граница исключительно, а нижняя граница ледующего интервала включительно.
Количественная однородность групп определяется по коэффициенту вариации:
ν=(σ/xср)×100%.
Если ν превышает 33%, то выделенная группа признается количественно неоднородной и наоборот.
Неравные (специализированные) интервалы широко применяется при построении типологических группировок.
При построении интервальных рядов распределения по дискретным признакам обозначение границ интервала дается с разбежкой в 1.
5. Средние величины и способы их вычисления. Определяющее св-во средних.
Среди обобщающих пок-лей, к-рыми стат-ка характеризуют общ. Явления и свойственные им закон-сти, большое значение имеют средние величины. Это объясняется тем, что стат-ка изучает совокупности явл-ний по количественным признакам. В этой связи важно, чтобы средние величины были основаны на массовом обобщении данных в пределах их качественной однородности. Средней величиной в стат-ке наз-ся обобщающая хар-тика сов-сти однотипных явл-ний по какому либо варьирующему признаку, кот-рая пок-ет ур-нь этого признака на единицу сов-сти. Средняя величина одним числом характеризирует то общее, то типическое по изучаемому признаку, к-рое присуще всем единицам данной сов-сти. Средняя величина явл-ся относительно устойчивой хар-тикой изучаемых явлений. Поэтому она является одним из важнейших элементов выявления стат. закономерностей. Для устойчивого проявления действия ср. величин необходимо достаточно значительный объем сов-сти. важнейшим условием расчета средних является качественная однородность (типичность) сов-сти явлений. Поэтому предварительно необходимо произвести группировку данных. Особенность ср. величин заключается в том, что они являются абстрактными стат. хар-тиками, в тоже время они рассчитываются на основе конкретных реальных данных. Профессор И.С. Пасхавер полагал, что устойчивость средних заложена в самой качественной природе явлений, т.е. он выдвинул идею, регулирующую основу средних. Индивид. Уровни признака формируются под воздействием как основных глобальных причин, так и воздействием случайных индивидуальных. Для всесторонней хар-тики соц.-экон. явлений необходимо применять сис-му средних величин (общих и частных). Средняя, рассчитанная по разнородной сов-сти не имеет эконом. мысла и наз-ся общей средней. Применяя сис-му средних величин целесообразно дополнять их индивидуальными значениями (хmax, хmin), дополняя значениями моды и медианы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.