Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 28

1)  гиперболическая зависимость: здесь с изменением признака-фактора с замедлением изменяется прирост результативного показателя.

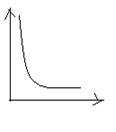
 Ŷ_х=а₀ + а₁1/х

Для нахождения параметров уравнения регрессии гиперболического вида (уравнение гиперболы) необходимо решить следующую систему нормальных уравнений:

nа₀ + а₁∑1/х=∑у

{

а₀∑1/х + а₁∑1/х²=∑у/х

2)  уравнение полулогарифмической кривой. В данном случае в начальной точке отсчёта изменения происходят относительно быстрее, чем в конечной точке отсчёта (с большими размерами значений признака-фактора)

 

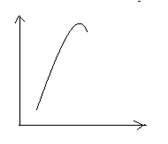
Уравнение полулогарифмической кривой имеет вид: ŷ_х=а₀ + а₁lgx

Система нормальных уравнений в этом случае будет иметь вид:

nа₀ + а₁∑lgx=∑У

а₀∑lgx + а₁∑( lgx)²=∑Уlgx

3)  уравнение параболы второго порядка: ŷ_х=а₀ + а₁х + а₂х²

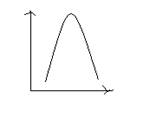
Для нахождения параметров:

nа₀ + а₁∑х + а₂∑х²=∑у а₀∑х +  а₁∑х² +  а₂∑х³=∑ху а₀∑х² +  а₁∑х³ +  а₂∑х⁴=∑ух²

В уравнении параболы второго порядка можно определить значение признака-фактора, при котором значение результативного признака достигает максимального значения. Для этого необходимо ур-е параболы второго порядка прировнять к нулю и найти первую производную по х.

(а₀ + а₁х + а₂х² )=0

а₁ + 2а₂х=0

х=(-а₁): 2а₂ первый параметр а.

Возможны и другие формы аналитического выражения в зависимости м/у результативным и факторным признаками (полиномы Чебышева более высоких порядков). Способ наименьших квадратов применим к уравнениям линейных полиномов.

65.Ур-ение множественной регрессии. Принципы отбора факторов уравнения регрессии.

М/у корлляц. и регресс. анализом существуют различия. При корелляц. анализе изуч-ся стахостические (случайные) связи. А при регресс. анализе условие случайности исходных данных во внимание не принимается. Здесь главным явл-ся то обстоятельство, что признаки-факторы должны быть относительно независимыми. При изучении закономерностей соц-эк-х явлений большое значение имеет выявление связи м/у этими явлениями. С этой целью строятся многофакторные регрессионные модели. Под регрессией поним-ся функция, предназначенная для описания зависимости изменения результативных признаков (У) в зависимости от влияния признаков-факторов (Френсис Гальтон). Основная цель ур-я множественной регрессии – построить модель (ур-е) с таким набором факторов, чтобы в основных чертах воспроизвести реальный процесс. Построение уравнения множественной регрессии включает в себя отбор факторов и выбор уравнения регрессии. При формировании многофак. регресс. моделей необходимо соблюдать (выполнять) ряд требований:

1)  при отборе факторов необходимо учитывать хар-р причинно-следственных отношений м/у явлениями, что позволит более полно раскрыть их сущность;

2)  значения как резуль-го (У) признака, так и факторных признаков должны быть количественно измерены;

3)  как признак-результат, так и признаки-факторы в эк-х исследованиях реальными статистическими показателями;

4)  в регрессионную модель следует включать наиболее существенные значимые факторы; значимость (существенность) факторов подтверждается либо F-критерием Фишера или критерием Стьюдента;

5)  признаки-факторы не должны находиться между собой в мультиколлинеарной зависимости;

6)  в регресс-ю модель нельзя включать факторы, выраженные удельными весами, сумма к-х равна единице. В этих случаях уравнение не имеет решения;

7)  целесообразно, чтобы признаки-факторы были выражены не объёмными показателями, а качественными. Качественные показатели сопоставимы м/у собой, т.к. они рассчитываются на единицу совокупности;

8)  при построении многофак. регресс. модели необходимо соблюдать условия, что статист. совокупность должна быть достаточно большой (и главно качественно однородной). Число единиц совокупности должно превышать число факторов регресс. модели примерно в 5-6 раз.

Многофакторная лин. регресс. модель имеет вид:

Ŷ=а₀ + а₁х₁ + а₂х₂ + …..+а_px_p;