Интерполяция производится исходя из предположения, что изменения в пределах периода, выражающее закономерность развития, относительно устойчивы. Для этого необходимо установить характер динамики, т.е. найти относительно устойчивые производные (средние) показатели: абсолютный прирост, темп роста и др.
Возможны различные варианты интерполяции:
1) рассчитывается средняя арифметическая из прилегающих пропущенному уровней ряда;
2) при условии арифметической прогрессии: 
(
)
3) при относительной стабильности темпов роста (геометрическая прогрессия)
, (
)
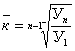4) производится выравнивание соответствующему уравнению тренда (при этом пропущенный уровень равен 0), а затем в ур-ние тренда подставляется порядковый номер фактора времени пропущенного уровня.
К примеру, используя первый способ интерполяции, определим его как среднюю арифметическую из уровней 2001 и 2003 гг.:
Произведем интерполяцию по второму способу расчета. Для этого необходимо вычислить среднегодовой абсолютный прирост за 2000-2004 г.:
Уровень 2002
г. определим: 
Интерполяция по третьему способу требует предварительного расчета среднегодового темпа роста за 2000-2004 гг.:
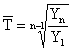Уровень 2002
г. составит:
35. Расчет средних абсолютных уровней по интервальным и моментным рядам динамики.
Особенности средних показателей рядов динамики состоит в том, что они рассчитываются на единицу промежутка времени (хронические средние).
Средние показатели абсолютных уровней по интервальным и моментным динамическим рядам рассчитываются по-разному.
Средний уровень интервального ряда динамики можно подсчитать по формуле:
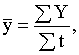где у – уровни интервального
динамического ряда;
t – длительность отдельных интервалов времени.
Если интервалы в ряду динамики равные, то формула расчета среднего уровня принимает вид:
где n – число равных промежутков или интервалов.
По моментным рядам динамики средний абсолютный уровень рассчитывается по-разному, в зависимости от характера исходных данных. Если уровни моментного ряда динамики даны на даты равноудаленные друг от друга, то в этом случае используется формула расчета среднего уровня вида:
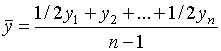
В данной формуле расчета среднего абсолютного уровня знаменатель совпадает с числом интервалов (кварталов), охватываемых рядом. Он меньше на единицу количества данных уровней, так как первый и последний уровни входят в расчет с половинными весами.
В тех случаях, когда уровни моментного ряда отстоят друг от друга на разном расстоянии (во времени), то в этих случаях необходимо полусуммы уровней взвешивать по величине интервалов времени между ними:
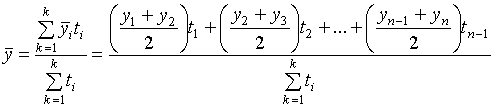, где k = n-1.
Если располагаем исчерпывающими данными об изменении изучаемых явлений, то расчет среднего абсолютного уровня по таким моментным рядам рассчитывается по формуле средней арифметической взвешенной:
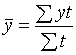,где у – уровень моментного ряда
динамики;
t – интервалы (промежутки) времени между ними.
36. Расчет среднего абсолютного прироста и среднего темпа роста
Уровни и аналитические показатели динамики измен-ся во вр-ни. Поэтому для обобщающей хар-ки ряда динамики (РД) в целом используются средн. вел-ны: ср. ур-нь, ср. абс. прирост, ср. темп роста и прироста. Средний абсол. прирост показывает, на сколько ед. в среднем изменился уровень РД за соотв-щий период времени:
или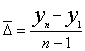 
; m=n-1, n –
число уровней РД, 
- цепн. абс. приросты. Средний
темп роста рассчит-ся посредн. геометр-ой из цепных темпов роста,
выр-ных в коэф-тах:
- с равными отрезками времени:
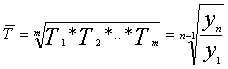
- с неравными
отрезками времени (средн. геометр. взвешенная): 
Средний темп
прироста показывает, на
сколько % в среднем за ед. времени измен-ся уровень РД: 
В тех случаях, когда известен только базисный ур-нь и сумма ур-ней за весь период расчет средней геометрической отличается от традиц. Формулы. Средний темп роста, определяемый по сумме уровней назван профессором Л.С. Казинцом параболистическим темпом роста. Он исчисляется след. образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.