Если порядк. номера рангов совпадают, то берется их среднее арифм-ое.
2. Коэф-нт конкордации – применяется для измерения тесноты связи при наличии 3х и более признаков.
, где m- число
признаков
S- сумма
квадратов отклонений рангов: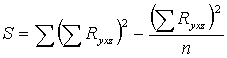 
3. Коэф-нты ассоциации и контингенции: используются для измерения тесноты связи, укладывающиеся в четырехпольную табл.(2*2) (в пределах признаков: да/нет).
|
a |
b |
|
c |
d |
В клетках табл. приводятся частоты распределения
единиц совокупности.
Коэф-нт ассоциации рассчит-ся: 
Относительно значимой хар-кой тесноты связи в этом случае явл-ся, если rассоц.>=0,5, ниже-слабая связь.
Коэф-нт контингенции (по табл.): 
rконт. >=0,2
4. Если каждый из кач-ых признаков состоит более, чем из 2х групп, то в подобных случаях для определения тесноты связи применяется коэф-нт взаимной сопряженности Пирсона:
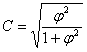, где 
- показатель взаимной сопряженности.
Русский статистик Чупров предложил исчислять коэф-нт взаимной сопр-сти по формуле:
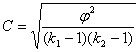
5. Для определения наличия связи применяется коэф-нт Фехнера:
, где С- совпадение
знаков отклонений значений как результат., так и факторн. признаков от средн.
арифметич. значения
Н- несовпадение знаков отклонений
53. Взаимосвязь агрегатных индексов. Принципы выбора периода весов при построении агрегатных факторных индексов.
Индексный метод анализа базируется на системе взаимосвязи показателей. Исходной посылкой этой взаимосвязи является – произведение признаков-факторов должны находиться в строго функциональной зависимости с результативным пок-лем ( мультипликативная модель). Индексные связи результативного и факторного пок-лей могут быть различными:
1. мультипликативные модели (произведение признаков-факторов дает результативный показатель)
2. аддитивные модели (сумма элементов-факторов дает рез-ный пок-тель)
3. смешанные модели (аддитивно-мультипликативные)
Рассмотрим принципы построения двухфакторной мультипликативной индексной модели. В кач-ве иллюстрации возьмем след. взаимосвязь эк-ских пок-лей:
Стоимость продукции(выручка)=Цена одного изделия * Кол-во реализованных изделий
Wpq = P * Q
Взаимосвязь между относит. пок-лями выражается теми же пропорциями, что и взаимосвязь между абсолютными.
Ipq = Ip * Iq
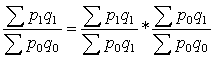
При построении системы взаимосвязанных агрегатных индексов вопрос о выборе периода весов в теории статистики рекомендательно решается так:
а) если в агрегатных факторных индексах в качестве индексируемой величины (сравниваемая) выступают качественные ( интенсивные: цена, урожайность, рентабельность и др.) признаки, то в таких факторных агрегатных индексах условно-постоянные веса рекомендуется брать на уровне текущего (отчетного) периода.
б) в агрегатных факторных признаках объемных пок-лей (экстенсивных) веса берутся на основе базисного периода.
Приведенная схема взаимосвязи факторных агрегатных индексов предполагает, что один из факторных признаков строится по отчетным весам, а др. – по базисным. Этот метод явл. схемой полной взаимосвязи индексов. В эк. анализе такой подход называют методом последовательного цепного индексирования.
Вычитая из числителя индекса его знаменатель получим пок-ли его абсолютных приростов:
pq
= 
в том числе:
pq(p) = 
pq(q) = 
Значит: pq
= pq(p) + pq(q)
Общий прирост рез-ного пок-ля в разрезе влияния факторов получим по схеме:
Поделив пок-ли абсолютных приростов по факторам на общую величину прироста получим пок-ли удельных весов (долей) абсолютного прироста:
Ipq= Ip * Iq ; Ip=Ipq / Iq ; Iq=Ipq / Ip ;
Рассмотрим следующ. модель взаимосвязи признаков:
Затраты на пр-во(издержки) = Себестоимость 1го изделия * Кол-во изделий
Wzq = Z*Q
Izq = Iz * Iq ; или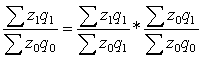 
Агрегатные индексы – основная форма общих индексов, т.к. они построены по взаимосвязи эл-тов модели. Рассмотрим след. трехфакторную индексную модель:
Матер-ные затраты на пр-во=Цена нормы расхода сырья *Норма расх. сырья *Кол-во изделий
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.