В основе
многофакторных (мн-х) индексов лежат множественные взаимосвязи соц-экон-х
явлений. Подобные связи рассм-ся на основе мн-х моделей. Модели взаимосвязи признаков
можно классифицировать по 3 направлениям:1. Мультипликативные модели.2.
аддитивные. 3.смешанные (аддитивно-мультиплиактивные).При построении мн-х мультипликативных
моделей необходимо, чтобы произведение признаков-факторов давало бы значение
результативного показателя. При этом произведении этих факторов должно отражать
экон-е содержание явлений. Последоват-ть расположения ф-ров в мн-й индексной
модели должно быть строго детерминированной (в данном случае не допускается
произвольная перестановка факторов местами). Возможны различные варианты построения
мн-х индексных моделей: а)на 1 месте стоит объёмный (экстенсивный)
признак-фактор(
) б) на 1 месте стоит качественный(интенсивный)
признак-фактор. Напр.
В зависимости от характера мультипл-х моделей они
по-разному решаются. Рассмотрим принципы решения каждого из предл-х видов
моделей. на 1 месте стоит объёмный (экстенсивный) признак-фактор: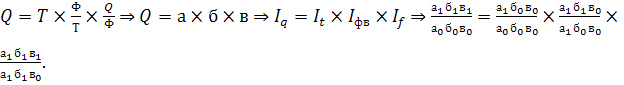 
(фв-фондовооруж-ть,
f-фондоотдача). Показатели абсолютных приростов традиционным спос-м
получим: 
В том числе 
; 
; 
. В теории статистики разработан алгоритм расчёта
показателей абсолютных приростов применительно к индексным моделям, где на 1
месте – объёмный пр-к-фактор. Он имеет следующую схему: 
; в том числе 
. Показатели темпов прироста в этой схеме опред-ся
так: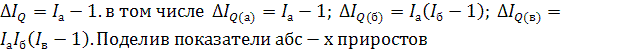 
по
факторам на величину общего абсолютного прироста, получим схему определения
удельных весов абс-го прироста. Рассм-м мн-ю индексную модель и принципы её
решения для случая, когда на 1 месте ст-т качественный(интенсивный)
признак-фактор. Рассм. 4-факторную индексную модель производит-ти труда: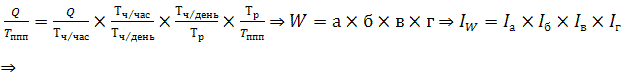 
Вычитая из числителя к-го индекса его знаменатель,
получим показатели абс-х приростов: 
. В том числе 
; 
(
)
; 
; 
. Алгебраич-й алгоритм решения мн-х индексных моделей,
где на 1 месте стоит кач-й пр-к-фактор таков: показ-ли абсол-х приростов
опред-ся по схеме: . В том числе: 
; 
; 
; 
Схема определения темпов прироста по факторам такова:
-1. В том числе 
; 
; 
; 
.
Рассмотренная индексная модель анализа производит-ти труда явл неполной
(усечённой моделью): 
. Чтобы получить полную индексную модель объёма
продукции необходимо правую и левую часть 
на численность работников и т. о. получим модель
анализа динамики Q продукции за счёт изменения численности работников и
производ-ти труда, а динамика произв-ти труда представлена произведением 4-х
факторов. В связи с этим представляется возможным исследовать динамику Q
продукции в разрезе влияния производит-ти труда Q=T
. Схема анализа динамики Q
продукции за счёт изменения числ-ти работников и за счёт изменения ф-ров производит-ти
труда будет выглядеть так: 
=
. В том числе а) 
; б)
. Из этого 
; 
; 
; 
. Отношение абс-х приростов к ур-ню базы сравнения (
), получим показатели относит-х приростов. Поделив
пок-ли абс-х приростов по фак-рам на общий абс-й прирост, получим характ-ки
стр-ры абс-х приростов.
По двухфакт-м индексным моделям показатели стр-ры приростов на основе
относит-х показателей приростов определяются по схеме: 
; 
61. Принципы построения террит-х индексов прямым и косвенным способами. Взаимосвязь террит-х индексов.
Для пространственных сопоставлений используются территориальные индексы. Их особенность состоит в том, что они рассчитываются в двух вариантах (район А к району Б, и наоборот). Рассм-м принципы построения агрегатных факторных террит-х индексов(индекс цен и физич. объёма продукции).
; 
; 
; 
.
Агрегатный факторный индекс физического объёма строится по формуле:
; 
; 
.
Приведенные формулы расчета тер-х индексов относятся к прямому методу. Кроме прямого метода расчёта тер-х индексов сущ-т и косвенный. Он состоит в следующем: тер-й индекс цен рассчитывается по косвенному методу так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.