1) относительная вел. планового (установленного) задания
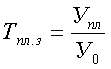Т – темп планового задания, У0 –
уровень базы сравнения; Упл – абсол. размер установленного задания.
2) относительная величина степени выполнения плана
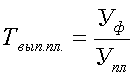
3) относительная величина фактической динамики:
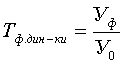
Приведенные показ-ли темпов роста взаимосвязаны между собой след. образом:
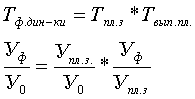
4) относительные величины структуры (удельного веса)– рассчитываются отношением части совокупности к общему итогу (доля, удельный вес).
5) относительные величины интенсивности – дают хар-ку распространенности (интенсивности) какого-либо специфического явления в той среде, где оно находится.
Коэф-т рождаемости=
(Р – кол-во родившихся, 
-среднее кол-во нас-ние )
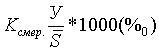(У – кол-во умерших, - среднее кол-во нас-ния )
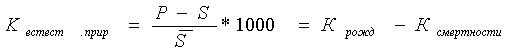
6) относительные величины координации – рассчитываются путем сравнения частей целого. (коэф-т феминизации = колво муж/кол-во жен).
7) относительные величины сравнения. Здесь сравниваются одноименные показ-ли за один и тот же период, но по различной территории (пространственные сопоставления)
8) относительные величины факторного анализа рассчитываются в виде различных коэффициентов и т.д.
Широкое распространение относительные величины находят в индексном анализе, где они рассчитываются по взаимосвязанным показателям; в экономико-стат. анализе необходимо абсолютные относительные величины применять комплексно (системно).
12. Абсолютные показатели рассеивания (вариации)
Вариация – кол-ные различия различия значений признака по отдельным единицам сов-сти или их групп.
К абсолютным показателям вариации относятся:
1. Размах вариации: 
2. Среднее линейное отклонение рассчитывается по формулам:
а) по несгруппированным данным: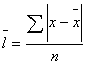 
где
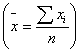
б) по сгруппированным данным: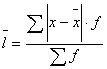 
где
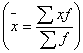
Среднее линейное отклонение – величина именованная, выражается в тех же
единицах измерения, что и значение признака. Недостаток этого показателя в том,
что он дает ТОЛЬКО оценку величины колеблимости признака, не указывая на
направление колеблимости (
). Для преодоления
противоречивости формулы среднего линейного отклонения необходимо эти
отклонения возвести в положительную степень (наименьшее значение этой степени -
квадрат).
3. Дисперсия признака: средний квадрат отклонений значений признака от средней называется дисперсией.
а) по несгруппированным данным: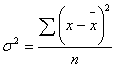 
где
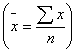
б) по сгруппированным данным (по рядам распределения):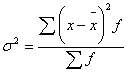 
где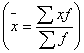 
.
В результате математических преобразований значение дисперсии можно вычислить и по другому:
а) по несгруппированным данным: 
где
б) по сгруппированным данным: 
где
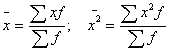
Дисперсия признака – число отвлеченное (не имеет единиц измерения)
4. Корень квадратный из дисперсии – среднее квадратическое отклонение:
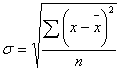где 
- по
несгруппированным данным.
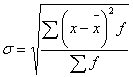
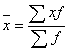- по сгруппированным.
Среднее квадратическое отклонение – величина именованная. Она имеет
единицы измерения значения признака. Среднее квадратическое отклонение дает
характеристику как величины колеблимости признака, так и знака направленности (). Тогда можно записать: 
.
Особенность дисперсии 
состоит в том, что ее
можно разложить на составные части, что является основанием фактора
дисперсионного анализа.
5. Оценкой квартильной характеристики колеблимости признака является
значение q, рассчитанной по формуле: 
- квартильная
характеристика оценки колеблимости признака (Q).
13. Относительные показатели рассеивания (вариации)
Относительные показатели вариации:
1 коэфф-т остилляции;
2 коэфф-т среднего линейного отклонения;
3 коэфф-т вариации;
4 относит. пок-ль медианного отклонения;
5 коэфф-т асимметрии;
6 коэфф-т эксцесса.
;
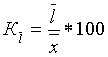- коэфф-т среднего линейного отклонения
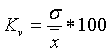- коэфф-т вариации
Относит. показатель квартильной хар-тики:
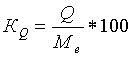, или
Важнейшим относит. пок-лем относит. оценки меры колеблимости признака явл-ся коэфф-т вариации. Принято считать, что если коэфф-т вариации превышает 33%, то данная совокупность по изучаемому признаку явл-ся количественно неоднородной и наоборот.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.