Средняя арифметическая:
1) связь между признаками представляется выражением: W=xf
2) просуммируем правую и левую части: ∑ W = ∑xf
3) при замене индивид. значения средней, согласно определяемому
свойству средней, равенство не нарушается: 
→ ∑ W = 
∑f → =
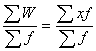
Средняя гармоническая:
1)
зависимость между
признаками определяется следующими выражениями: 
2)
3)
→ 
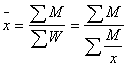
Средняя геометрическая:
1) Допустим, что общий результат есть значение признака: W=x
2) Возьмем применительно к этому выражению произведение значений: П - произведение П(W) = П(х)
3) При замене индивид. значений признака (х) их средними значениями выражение не нарушит равенства: П(W) = П()
4) П(W) =
5) 
Средний квадрат и средняя квадратическая:
1)
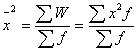- средний квадрат
4) 
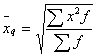- средняя квадратическая.
В каждом конкретном случае формула расчета среднего значения признака определяется экономическим содержанием взаимосвязи признаков и исходным соотношением расчета средней величины.
Например, затраты на производство зерна (З) можно представить произведением трех признаков: себестоимости 1ц зерна (z), урожайности зерновых (у) и размера посевной площади. Взаимосвязь указанных признаков через символы будет выражена: З= z у П
Уровень урожайности зерновых культур определим по
формуле: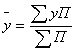 
, а средний уровень себестоимости 1 ц
зерна на основе взаимосвязи признаков будет равен: 
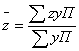, где
уП – валовой сбор зерна.
11. Методология расчета статистических показателей. Система абсолютных и относительных статистических показателей
Основу представлений об экон. явлениях и процессах, их своеобразии, о ста. Хар-ре закономерностей дает сис-ма стат. обобщающих показателей.
Стат. показатель – это количественная хар-ка отдельной стороны соц-экономич. явления.
Стат. показ-ли отражают качественность содержания явлений.
Количественная х-тика отдельной стороны или нескольких сторон соц.-экон. явления с учетом их качественного своеобразия и дает представление о стат. пок-ле. Исходной основой стат. пок-ля явл-ся абсол. стат. величины. Они характ-ют размеры (объемы) и ур-ни соц.-эк. явлений. Различают: игдивидуальные и общие (итоговые) абсол. величины. Индивид-ные абсол. величины получаются в рез-те регистрации данных при проведении стат. наблюдения. Итоговые абсол. величины получаются в процессе ста. сводки, при к-рой объемные ста. величины (экстенсивные) в случае одинаковых единиц измерения поддаются прямому непосредственному суммированию. Все абсол. величины имеют рамерность, т.е. единицы измерения. Виды един. Измерения: а) натуральные (когда учитываются потребительские св-ва), б) условно-натуральные (например, все виды кормов пересчитываются в кормовые единицы по определенному коэф-ту (за единицу пересчета берется 1 кг овса, его потребительские св-ва), тракторы по мощности пересчитываются в эталонные 80-сильные) в) комбинированные (тонна/км, киловатт чел/час), г) стоймостные пок-ли. Многие объемные абсол. пок-ли определяются расчетным путем. ВВП=ВВ(валовый выпуск) – ПП (промежуток потребления).
Качественные (интенсивные) стат. пок-ли явл-ся расчетными хар-тиками. Они отражают урнь пок-ля на единицу сов-сти. Например, Ур-нь производительности труда, с/с ед. продукции. Интенсивные абсол. величины нельзя непосредственно суммировать. Для их расчета по группе объестов необходимо просуммировать объемные абсол. величины по их числителю и знаменателю для всесторонней х-тики (анализа) соц. Эк. явлений необходима сис-ма абсол. пок-лей (объемных и качественных), а также сис-ма относит. стат. величин.
Относительные стат. величины
Они рассчитываются на основе различных сопоставлений (сравнений) абсолютных величин, а также в результате комбинаторных расчетов ранее исчисленных относительных величин.
Связь между относительными величинами выражается теми же соотношениями (характером связи), что и связь между самими абсолютными величинами.
В зависимости от характера сравнения рассчитываются различные виды относительных величин:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.