Значения моды,медианы и квартильн.хар-тик,а такж6е децильн.хар-тик относ.к разряду непараметрич.средних.Модой в ст-ке наз.значение признака,имеющее наиб.частоту(вес)распределения.По дискретным данным значение моды опред-ся видуально.Значение моды по интерв.вариац.рядам опред-ся по формуле:
Мо=xmо+imo*fmo– fmo-1 .
(fmo – fmo-1)+ (fmo – fmo+1)
Медианой(Ме)в ст-ке наз.значение признака у той единицы совокупности,к-рая делит упорядоченный ряд на 2 равные части.В интерв.вариац.рядах с равными интервалами значение медианы опред-ся по след.мат.формуле:
Ме=хme(н)+ime*∑f/2 – Sme-1
fme me=∑f/2
Если ∑f нечетное число,то берут ∑f+1
Sme-1- накопленные частоты домедианного интервала.
Графич.представление значения моды представим в прямоугольн.с-ме координат,где нанесем значения частот модальн.интервала,ему предшествующего и за ним следующего (fmo-1,fmo , fmo+1).Графич.представление моды выполним,опустив перпендикуляр на ось абсцисс из точки пересечения линий АС И ВД.
Графич.представление медианы также выполняется в прямоуг.с-ме координат,где по оси абсцисс приводятся значения,а по оси ардинат-масштаб накопл.частот.Здесь изображается кривая накопл.частот(ее наз.кумулята или огива).Затем по оси ординат на границе полусуммы частот проводят линию,параллельн.оси абсцисс.Из точки пересечения огивы с полусуммой частот опускают перпендикуляр на ось абсцисс.
Если в интервальн.ряду распределения набл.строгая симметричность,то в этом случае значения моды,медианы и средней совпадают. Если в интерв.рядах распределения набл.несколько значений моды,то такой ряд распределения явл. колличеств. неоднородным.В данном случае необх.перегруппировка данных по подсовокупностям.По принципу определения медианы можно рассчитать и др.стат.хар-ки.Так,квартильные значения ряда распределения(1/4часть,1/2=медиане,3/4).Значение 1-ой квартильн.хар-ки:
Q1=хQ1(н)+iQ1*∑f/4 – SQ1-1
fQ1
Значение 2-ой:Q2=Ме
Значение 3-ей: Q3=хQ3(н)+iQ3*∑3f/4 – SQ3-1
fQ3
Подобн.образом можно рассчитать децильн.хар-ки(10,20,30%....),а также пинтильные(50-ая,100-ая,200-ая,150-ая).
9. Функциональные средние. Мажорантность средних
Математ-ки выводят различные формулы средних из степенной формул вида:
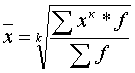
При к=1 получим среднюю арифметическую
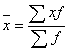
При к=-1 получим среднюю гармоническую
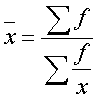
При к=0, использую правило Лапиталя док-но, что при к=0 получим среднюю геометрическую
![]()
При к=2, получим значение средней квадратической
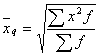
В зависимости от показателя степеней значения средних, исчисленных по одним и тем же данным, будут различаться. Подобная различимость средних называется их мажорантностью, которая выражается следующим неравенством:
![]()
Строго математическое положение мажорантности средних доказал А.Я Боярский на основе построения функциональных средних. Он предположил следующую функцию определения средней:
Ф(Х) = хk
Рассчитывая для различных значений степеней k
соотношения второй производной к первой производной 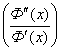 определим
числовые выражения значений средних.
определим
числовые выражения значений средних.
При k=1 получим значение средней арифметической.
Ф (х) = х Ф' (х) = 1 Ф" (х) = 0 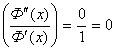
При k= -1:
Ф (х) = ![]() Ф' (х) = –
Ф' (х) = – ![]() Ф" (х) =
Ф" (х) = ![]()
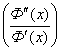 =
=![]()
При k=0: Ф(х) = lg x
В результате соотношения второй и первой производной по этому выражению
получим 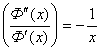
Для степенной средней Ф(х)=хkее порядок определяется

Согласно численным значениям различных средних, установленных профессором Боярским, мажорантность средних можно записать так:
![]() .
.
В мат. стат-ке доказано, что теоритические выражение средней величины есть ее мат. ожидание.
![]()
По эмпирическим данным
![]()
![]()
Дисперсия признака в мат- стат-ке опре-ся ![]()
![]()
![]()
10. Обоснование формул расчета средних на основе взаимосвязи признаков
Формулы расчета средней величины зависят от характера связей между признаками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.