Wsmq = S*M*Q
Ismq =Is *Im *Iq
или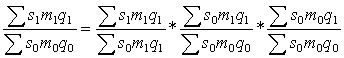 
В аналитических исследованиях нередко строят индексы (факторные) в изолированной схеме, т.е. все веса берутся на уровне базисного периода:
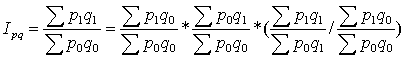
Для увязки системы факторных индексов в изолированной схеме (произведение факторных индексов давало бы результативный индекс), необходимо вычислить дополнительный индекс (индекс ковариации) –[Icov].
Индекс ковариации цен исчисляется так:
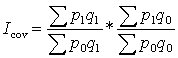; и Ipq= Ip(базисн. веса) * Iq * Icov
В данной схеме общий абсолютный прирост рез-ного пок-ля не имеет полного разложения абсол. прироста по факторам из-за трудностей разложения неразложенного остатка.
54. Средние индексы.
Средние индексы являются формой алгебраического преобразования агрегатных факторных индексов. Используется средний арифметический и средний гармонический индексы.
Средний арифметический индекс – форма алгебраич. преобразований агрегатных факторных признаков объемных (экстенсивных) пок-лей:
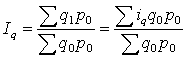
Если веса базисного периода по всем наименованиям индексного набора будут одинаковы, то средний индекс физического объема можно рассчитать по средней арифметической простой:
, тогда 
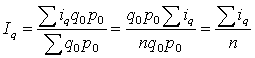
Cредний гармонический индекс явл. формой алгебраического преобразования агрегатных факторных индексов в качественные (интенсивн.) пок-ли, т.е.:
, 
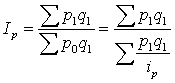Органы стат-ки, как правило, индексы цен сплошным способом не рассчитывают. Аналогом индекса цен явл. «товары-представители». Такой способ расчета индекса цен наз-ся дефлятированием.
55. Анализ динамики средних уровней: индексы переменного, постоянного составов и индекс структурных сдвигов.
Одна из задач, кот. решается при помощи индексов – это выявление роли влияния структурных факторов на динамику результативных пок-лей.
Индекс переменного состава рассчитывается в рез-те сравнения средних ур-ней отчетного и базисного периода кач-ных пок-лей. При этом, такой способ сопоставления имеет смысл в том случае, когда средние уровни отчетного и базисного периодов рассчитаны по сгруппированным данным, т.е. есть зн-я признака и веса.
Так, например, индекс себестоимости переменного состава:
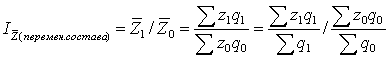
На индекс переменного состава влияют 2 фактора:
1. непосредственное изменение ур-ней самого индексированного признака (Zi )
2. изменение структуры весов (доли единиц совокупности
кажд. подразделения в общем итоге) -> [di(q) =qi / 
=> 
= 1,0]
В аналитическом исследовании при помощи индексов выделяется влияние каждого из факторов на динамику среднего пок-ля. Для этого исчисляются индексы себестоимости постоянного (фиксированного) состава и индекс структурных сдвигов.
Индекс себестоимости постоянного состава: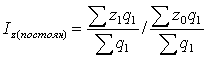 
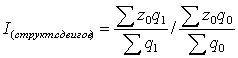
Таким образом: 
=
*
Если при расчете средних пок-лей вместо абсол. весов qi взять доли di , то получим след. представление расчета индексов пост., переем. составов и структ. сдвигов:
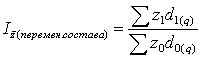
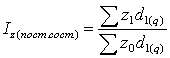
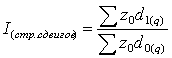
Таким образом: =*; или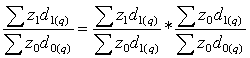 
Вычитая из числителя кажд. индекса его знаменатель получим схему разложения общих абсол. изменений среднего ур-ня засчет составляющих факторов.
Абсолютное изменение средней себестоимости определим:
, в том числе:
а) Абсолютные изменения средней себестоимости в
результате непосредственного изменения самих ур-ней себестоимости: 
= 
б) Абсолютные изменения средней себестоимости в результате изменения структуры весов:
= 
Т.е. общее изм. равно: 
60 Принципы построения и решения (алгоритмы) многофакторных индексных моделей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.