Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 13

При многоступ. выборке отбор производ-ся поэтапно (по стадиям). Каждая стадия отбора имеет имеет свою единицу отбора. На 1-х этапах произв-ся отбор укрупнен. Пакетами (комплектами), а на последнем этапе произв-ся непосредств. отбор ед-ц совок-ти. При этом на кажд. стадии опред-ся ошибка выборки.При этом способе берётся комбинация выборки. Допустим, серийной с индивид. Генер. совок. разбив-ся на равновеликие серии. На 1 этапе отбир. серии, а на 2 – из отобр. серий произв-ся индив. выборка. В данном случае стат. х-тики выборки рассчитываются на каждом этапе.

Применительно к нашей модели выборки х-тики рассчитывются по формулам: Ср. ошибка выборки:а) при повторн. отбор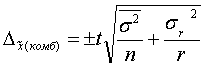е: ;  где  - средняя из серийных дисперсий.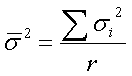  

б)при бесповт. отборе: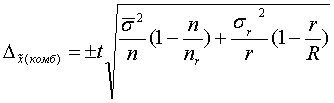, n_r- общ. число ед-ц в отобр. сериях.

Моментно-выборочн. наблюд-е – это вид выборки связанный с изучением процесса во времени. Здесь единицей отбора явл-ся «момент наблюдения». По времени этот вид наблюдения явл-ся выборочным, т.е. регистрируется состояние «моментов наблюдений», допустим, с отметкой «Р_абота» «П_ростой», а по регистрации данных относительно всей совокупности.

На основе моментно-выборочных наблюдений изучается стр-ра рабочего времени, раб. Оборудования и т.д. Всязи с этим здесь определяются только ошибки доли, только при повторном отборе.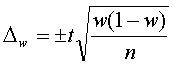

При данном способе отбора численность ген. сов-сти неизвестна.

24. Определение объёма (численности) выборочной совокупности.

При организации выбор. наблюд-я необх. решить пробл. опред-я необх. численности выборки (n). Формулы опред-я необх. числ-ти выборки вывод-ся из формул предельн. ошибок выборки. Опред-ая числ-ть выб. зависит от ряда условий: 1)от меры колебл-ти изуч-ых признаков (σ²); 2)от степени точности оценки пар-ов выборки (вероятность) 3)от заданной величины пред. ошибки выборки (отΔ); 4)от видов и способов выборки.5)от численности генер сов-ти

Формы определения числ-ти выборочной совок-ти:

1.Собств-случ выборка: а) повт.отбор  (для средней) (для доли)

б)бесповт.(для средней), (для доли)

2.Типическая выборка: а)повт  (д/средней), (д/доли) б)бесповт 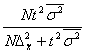(ср)

(доля)

3. Серийная выборка а)повт (ср), для доли отсутствует, б) 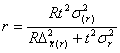(ср.), для доли отсутствует.

При опред-и числ-ти выборки возник. ряд вопросов: 1) неизвестна дисперсия признака σ². Её опр-ют разл. способами прикидок. Берётся дисперсия по аналог. выборкам, проведённым ранее. 2) Известно, что 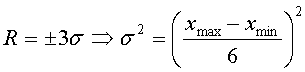; (чисто математически)

3) Для нахождения σ² проводят пробные экспресс-выборки.     4) При опред-и дисперсии доли берут её max значение (0,25).

25. Малая выборка

К безусловно малым относятся выборки с объемом сов-ти менее, чем 30 набл-ний.

Если в больших выбоках закон распределения определяется по переменным значениям t, то при малых выборках закон распредел. зависит от распределен. значений вел-ны t и от объема совокупности(выборки). Д/оценки возможных пределов малой выб-ки примен-ся отношение Стьюдента.

где ,

З-н распр-ния величины t носит название закона распределен. Стьюдента. Согласно кот. плотность распределения ошибок малой выборки определяется:

Вер-ть того, что при заданном объеме выб-ки (n) значение t будет не больше заданной tф определ-ся интеграл/ фун-ией.

где С- постоян. величина, кот. определ-ся взависим-ти от числа степеней свободы. С помощью гаммафункции:

Значение распределен. Стьюдента(S(t,n)) табулированы и приведены в соответсв-их табл-ах, кот. облегчают применения отношении t на практике.

На основе этих табл. представл. возможным установить вер-ть того, что факт-ая отошение tфи  не больше приведенного табл. значения t, т.е. вер-ть что, tфи будет меньше

Табл. значен. t определ-ся с заданным ур-ем значимости  и числом степеней свободы(v).

На осн-ве малой выб-ки реш-ся след-ие задачи:

1) определ-ся границы(пределы) среднего значен. признака по генеральн. совок-ти