Отметим, что в силу слишком большой неоднородность изучаемой совокупности по исследуемому признаку v может превышать 100%.
Подмечено, что зав-сть м/д средним квадратическим отклонением и средним линейным отклонением выражается пропорцией (приближенно):
Абсол. и относит. пок-ли вариации широко используются в эк-ко-стат. анализе. В частности при оценке устойчивости (равномерности) изучаемых процессов применяется коэфф-т устойчивости (равномерности).
Показатели равномерности (устойчивости) исп-ся пр оценке поставок, при оценке устойчивости с/х, производстве и т.д.
14. Расчет дисперсии (среднего квадратического отклонения) по интервальным вариационным рядам на основе комбинации условных моментов.
По интервально-вариационным рядам с равными интервалами значение дисперсии можно определить по преобразованной формуле, используя комбинацию условных моментов первого и второго порядков.
Известно, что значение дисперсии можно определить из след. выражения:
Вычитаем из каждого значения признака (хi) постоянную величину А и поделить эти отклонения (хi - А) на кратную величину к, в результате подобных преобразований получим:
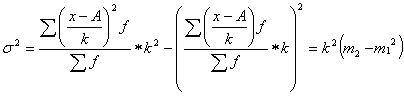
Значения дисперсии в преобразованном виде можно представить так:
Таким образом, 
15. Способы разложения общей дисперсии. Эмпирические коэфф-ты детерминации и корреляц. отношения.
Вариация (кол-ные различия) результативных признаков формируется под влиянием различных источников воздействия (факторов).
В стат-мат. лит-ре разработаны приемы анализа вариаций результат. Признаков от вариации факторных признаков. Основой такого анализа явл-ся разложения общей дисперсии результативных признаков на составные дисперсии этих признаков под воздействием вариации факторных признаков. Этот раздел мат. стат-ки явл-ся основой дисперсионного факторного анализа.
На основе методов дисперс. анализа представляется возможным определить значимость (существенность) влияния факторных признаков на результативные показатели (в частности на основе методов диспер. анализа устанавливается существенность факторных признаков положенных в основу группировки).
Метод дисперс. анализа предполагает выделение групп (группировку) по факторному признаку (признакам) с последующим сочетанием этих групп (выделяемых по факторному признаку) с результативным признаком.
Значение результативного признака обычно обозначается символом У, а значение факторного признака (признаков) – X, Z, V.
В простейшем виде общая дисперсия результативного признака (
) расчленяется на две составляющие
дисперсии.
а) межгрупповую дисперсию 
б) внутригрупповую дисперсию 
Таким образом, в мат-стат-ке доказано, что правило сложения дисперсий можно записать так:
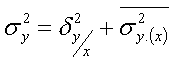- однофакторная дисперсионная модель.
Здесь группировка произведена по одному факторному признаку. В мат.
стат-ке внутригрупповая дисперсия считается дисперсией остатков (прочих)
неучтенных факторов и обозначается 
.
В данном варианте правило сложения дисперсий реализуется на основе эмпирических данных, т.е. предварительно по проведенной группировке по факторному признаку в сочетании с результативным признаком.
Общая дисперсия результативных признаков формируется под воздействием вариации с факторов.
Общая дисперсия результативных признаков рассчитывается по совокупности в целом (без предварительного разграничения ее) на группы по факторному признаку.
Способы расчета общей дисперсии:
а) по несгруппированным данным по результативному признаку
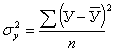, или
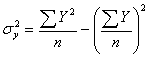
б) по сгруппированным данным
, или
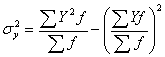
Если исходные данные по результативному признаку представлены
интервальными вариационными рядами с равными интервалами, то значение дисперсии
результативного признака 
может быть расписана
по способу условных моментов.
Межгрупповая дисперсия учитывает вариацию результативного признака, определяемую вариацию факторного признака (признака положенного в основу группировку).
Межгрупповая дисперсия рассчитывается:
, где 
- среднее значение результативного
признака по каждой из групп, выделенных по факторному признаку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.