Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 14

2)дается оценка значимости расхождений выборочных средних. По формуле:

где  x1, x2 – ср. значения признака по каждой из 2-х выборок; n1,n2 – объемы совокупностей по каждой из выборок S- среднее квадраты. отклонения разности средних;

Д/оценки значимости расхожден. выборочных средних сранив-ся tфи(эмп.) с tтабл. и если tфи> tтабл, то расхожден. между выборочными средними признаются существен-ми и наоборот.

tтабл определ-ся по таблиц. Стьюдента с заданным ур-ем значимости  и числом степеней свободы v = n1+n2-2

Суммы квадрата отклонений значен. признака от средней:

26,27 Сравнительные оценки раз-ий выбор.характеристик д/случая больших(малых)выборок

В практике выборочных исследований возникает необходимость сопоставления и оценки на существенность выборочных характеристик, рассчитанных по двум совокупностям. Проблемные оценки расхождений и их значимост. связано с тем, что выборочн. показатели полученные по 2ым выборкам из одной и той же генеральн. совокупности различаются. Важно установить являются ли эти расхождения существенными или незначительными.(связанными с особен-ми ошибок выоборки). Д/сравнительн. оценки значимости(или незначимости) расхожден. выборочных показателей используют спец. t-критерий. 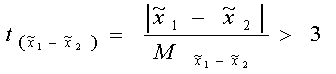, то различия между выборочными средн. показателями признаются сущест. значимыми и наоборот.

Средняя ошибка разности определяется по формуле: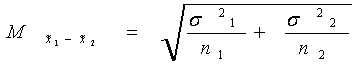

Применительно  к оценке расхождения долей критерий t определяет. по фор-ле:

Средняя ошибка разницы долей:

Вероятностн. оценка расхождений выборочных хар-ик(средних долей)

осуществ-ся по след. схеме:

Если с заданным уравем значимости(обычно берется 5% уровень значим-ти)т.е. АЛЬФА=0.05 сравнив-ся t_эмп.(расчит. по вышепред. формулах) сравнивается с t_табл., кот. нах-ся по табл. Стьюдента. Д/этого необход-мо задать ур-нь оценки значимости и числом степеней свободы(v=n₁+n₂-2)

Если tэмп> tтабл., то расхожд. между выборочн. показателями признаются существенными.

28.Способы распространения выборочных х-к на данные всей сов-ти.

Основная задача выборочного метода исследования состоит в том, чтобы перейти на основе показателей выборки к оценке показателей генер. Сов-ти, опр-ляя границы средней и границы доли. На ряду с этим статистика предлогает ряд специфических приемов распространения на всю совокупность:1. способ прямого (непосредственного) распространения; 2. способ поправочных коэффициентов. В первом случае границы оценки среднего показателя умножаются на численность генер.сов-ти(N). В р-те получим значения границ оценки итогового показателя по всей генер.сов-ти. Во втором случае способ применяется для уточнения данных сплошного наблюдения. Порядок действия таков: производится отбор выборочным путём из данных сплошного наблюдения (допустим, прведена выборка в каком-либо районесплошная перепись скота по индивидуальнымхозяйствам). Затем механически из данных сплошного наблюдения производится 10% выборка. В ней оказалась 500 голов коров, а вся численность по району N=5000 голов. Затем в этих же подворьях производится повторный обход и оказалось, что в этих хозяйствах 508 голов коров. Тогда Кпоправки=508:500=1,016 Затем данные сплошного наблюдения умножаются на поправочный коэф., т.е. N’=N*Кпопрвавки=5000*1,016

29.Схема однофакторного дисперсионного анализа.

Рассмотрим схему однофакторного ДА:

1.Вычислим значения сумм квадратов отклонения 3ёх видов:

1.1.общую сумму квадратов отклонений(в целом по изучаемому объему сов-ти)

1.2.сумму квадратов отклонений с учётом влияния факторного признака

1.3.сумму квадратов отклонений остаточного комплекса(влияние прочих факторов)

Выполняется условие . Общая сумма кв.отклонений рассчитывается в целом по результ. Признаку(здесь не производится разграничение сов-сти на группы по факторному признаку). На различия уровней результативного признака влияют множество причин(источников воздействия). Сумма кв.отклонений рассчитывается по ф-ле:, или , где N- общее число наблюдений. Обозначим , тогда -H;