На основе цепных абсолютных приростов можно рассчитать базисные абсолютные приросты. Для этого необходимо последовательно их просуммировать.
Темп роста – это отношение данного уровня к уровню, принятому за
базу сравнения. При расчете цепных темпов роста производится сравнение каждого
последующего уровня с предыдущим, то есть 
При
исчислении базисных темпов роста сравниваются каждый последующий уровень с
начальным, то есть 
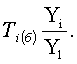
Темп роста выражается как в коэффициентах, так и в процентах и показывает, во сколько раз уровень данного периода превышает уровень базы сравнения.
На основе цепных темпов роста можно рассчитать базисные темпы роста. Для этого необходимо их последовательно перемножить. А от базисных темпов к цепным перейдем, если поделим каждый последующий базисный темп на предыдущий.
Темп прироста – это отношение абсолютного прироста к уровню, принятому за базу. При цепном подходе имеем:
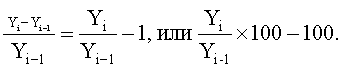При базисном способе
расчета темпа прироста будем иметь:
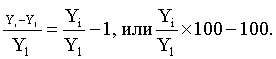
Темп прироста, как и абсолютный прирост может быть и положительным и отрицательным.
От цепных темпов роста к базисным перейдем последовательно их перемножая:
От базисных к цепным перейдем поделив каждый последовательный базисный темп на предыдущий.
Абсолютный размер 1% прироста – это отношение абсолютного прироста к темпу прироста, выраженному в процентах. Он показывает, какое содержание имеется в 1% прироста, насколько весом один процент прироста. Этот показатель целесообразно рассчитывать только по цепному методу, а именно:
Абсолютный размер 1% прироста =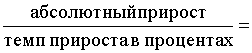 
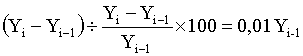
Таким образом, абсолютный размер 1% прироста равен одной сотой от уровня базы сравнения (0,01 Уi-1). Вычисление показателей абсолютного значения 1% прироста базисным способом не имеет смысла, так как в этом случае исходная база сравнения остается неизменной, (начальный уровень ряда) и тогда абсолютный размер 1% прироста будет во всех случаях сравнений одинаков (0,01У1).
Скорость абсол. прироста рассчит. Как вторые разности абсол. приростов.
Относит. Величины ускорения (замедления) рассчитываются различными способами: а) сравнением абсол. приростов за одинаковые промежуткм времени отчетного и базисного периода, т.е.
б) сравниваются темпы роста за одинаковые промежутки времени различных показ-лей:
в) сравниваются показатели темпов прироста. Подобные пок-ли наз-ся коэф-тами эластичности.
33. Статистические приемы смыкания рядов динамики.
Тенденции в развитии явлений выявляют уже производные показатели динамического ряда и динамические средние.
Для более детального изучения тенденций в развитии явлений необходимо использовать специальные приемы исследования.
В результате приведения рядов динамики к одному основанию и их смыкание тенденции в развитии явлений удается выявить элементарным преобразованием рядов.
В том случае, когда вывод о правильности развития в динамическом ряду мешает его несопоставимость, возникающая вследствие организационных изменений в течение изучаемого отрезка времени, допустим, территориальных, прибегают к смыканию динамического ряда. Для получения сомкнутого ряда, отражающего динамику изучаемого явления, принимаем за 100% данные как для последующих, так и предыдущих лет.
Здесь возможны такие варианты: - если часть ряда динамики представлена средними уровнями, а другая моментными уровнями, то целесообразно от моментных уровней перейти к средним показателям уровней; б) если часть ряда динамики рассчитана по различному кругу объектов или по различным территориям, то их опять же надо привести к одному основанию. В этих случаях поступают так: рассчитываются относит. показатели на стыке изменений. При этом новый уровень при стыковке принимается за 100% и все относит. показатели рассчитываются по отношению к этому стыковочному уровню.
Этот метод носит рекомендательный характер.
34. Статистические методы интерполяции уровней рядов динамики.
Интерполяцией называется приблизительный расчет недостающих уровней внутри однородного периода, когда известны уровни по обе стороны отсутствующего.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.