2.- при этом способе выравнивания теряются начальные и конечные ур-ни ряда;
3.- выбор вел-ны инт-ла сглаживания часто трудно обосновать. От этого зависит выбор формы кривой;
4.-тренд, полученный с помощью скользящих средних, не имеет количественной оценки.
40. Выравнивание (сглаживание) уровней рядов динамики по уравнениям трендов (способ наименьших квадратов-МНК)
Наиболее универсальным способом выявления осн. тенденции является
аналитич. выравнивание по соответствующим ур-ям тренда. В данном случае
зависимость между ур-ями ряда (У![]() ) и фактором времени (t
) и фактором времени (t![]() ) аналитически описывается каким-л. ур-ем тренда.
Фактор времени t
) аналитически описывается каким-л. ур-ем тренда.
Фактор времени t![]() обозн-ся порядк. номером периода времени.
Если изм-е уровней в ряду динамики происх. По з-ну арифметич.прогрессии(с
относительно стабильными абс.приростами), то такая завис-ть между ур-ями ряда и
фактором времени м.б. выражена ур-ем тренда прямой:
обозн-ся порядк. номером периода времени.
Если изм-е уровней в ряду динамики происх. По з-ну арифметич.прогрессии(с
относительно стабильными абс.приростами), то такая завис-ть между ур-ями ряда и
фактором времени м.б. выражена ур-ем тренда прямой: 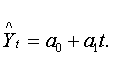 Если
же ур-ни ряда дин-ки возрастают(убывают) по з-ну геометрич.прогрессии (со
стабильными темпами роста), то такую зависимость между ур-ями ряда и фактором
времени можно описать ур-ем степенной ф-ции:
Если
же ур-ни ряда дин-ки возрастают(убывают) по з-ну геометрич.прогрессии (со
стабильными темпами роста), то такую зависимость между ур-ями ряда и фактором
времени можно описать ур-ем степенной ф-ции: 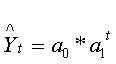 .Выявление
осн.тенденции в развитии явлений по способу аналитического выравн-я рассм.
Применительно к ур-ю тренда прямой:
.Выявление
осн.тенденции в развитии явлений по способу аналитического выравн-я рассм.
Применительно к ур-ю тренда прямой: 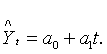 , где У-ур-ни
исх.ряда дин-ки,t-фактор времени, а
, где У-ур-ни
исх.ряда дин-ки,t-фактор времени, а![]() и а
и а![]() -пар-ры ур-я тренда; а
-пар-ры ур-я тренда; а![]() -усредненное знач-е нач.точки отсчета
движения, а
-усредненное знач-е нач.точки отсчета
движения, а![]() -коэф-т регрессии,показывающий на сколько
в среднем изм-ся ур-нь ряда дин-ки при изм-и фактора времени на ед-цу периода
времени(а
-коэф-т регрессии,показывающий на сколько
в среднем изм-ся ур-нь ряда дин-ки при изм-и фактора времени на ед-цу периода
времени(а![]() можно интерпретировать как
сред.абс.прирост,рассчит-мый по МНК).Для нахождения пар-ров ур-я тренда исп-ся
МНК т.е.
можно интерпретировать как
сред.абс.прирост,рассчит-мый по МНК).Для нахождения пар-ров ур-я тренда исп-ся
МНК т.е. ![]() . Для нахожд-я пар-ров ур-я тренда применит-но
к ур-ю прямой необх.решить след.сис-му норм.ур-ий:
. Для нахожд-я пар-ров ур-я тренда применит-но
к ур-ю прямой необх.решить след.сис-му норм.ур-ий: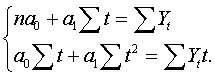 Приняв, что
Приняв, что ![]() , знач-я пар-ров опред-ся по формулам.
Получим:
, знач-я пар-ров опред-ся по формулам.
Получим: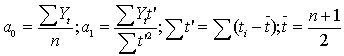 .
.
Если в ряду динамики нечетное число ур-ний, то ![]() нумеруется
-3, -2, -1 0, 1, 2, 3. Если четное- то -5, -3, -1, 1, 3, 5.
нумеруется
-3, -2, -1 0, 1, 2, 3. Если четное- то -5, -3, -1, 1, 3, 5.
Подставив в уранение вместо ![]() обозначенные
порядковые номера фактора времени получим выравненные (сглаженные,
теоритические) значения ур-ней ряда, при этом следует иметь в виду, что
обозначенные
порядковые номера фактора времени получим выравненные (сглаженные,
теоритические) значения ур-ней ряда, при этом следует иметь в виду, что ![]()
Вел-на колеблемости ур-ий ряда дин-ки опред-ся
сред.квадратич.отклонением (осн.ош-ка):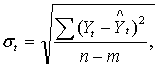 где n-число
ур-ий ряда,m-число пар-ров ур-я тренда.
где n-число
ур-ий ряда,m-число пар-ров ур-я тренда.
Относит. хар-кой меры колеблемости ур-ий ряда явл-ся коэф-т вариации: 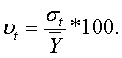
41.Статистическая оценка ускорения процессов развития эк.явлений (равномерное развитие).
Развитие эк.явл-ий может происходить по различ.з-нам. Здесь важно дать содержат. оц-ку рез-там мат.расчетов. Из всего многообразия з-нов развития рассм-ся 4 типа:1.равномерное развитие;.
Равномерное развитие, т.е. движ-е осущ-ся по з-ну арифметич.прогрессии
с постоянным абсолютным изм-ем ур-ий динамич.ряда. Эталонной моделью развития
этого типа служит ур-е равномерного движ-я. Этому типу движения соответ-т ур-е
тренда прямой вида: 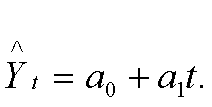
Если ![]() , то происходит равномерное
возрастание;если
, то происходит равномерное
возрастание;если ![]() , то равномерное убывание.
, то равномерное убывание.
2.равноускоренное(равнозамедл.) разв-е;
3.развитие с переменным ускорением(замедлением);
4.разв-е по з-ну с постоянным темпом роста
42. Статистическая модель оц-ки равноускоренного (равнозамедл.) развития.
Равноускор-е (равнозамедл-е) развитие, т.е с постоянным во времени
ускорением (замедлением). Эталонной моделью служит парабола 2-го порядка:![]() . Если
. Если ![]() >0
–ускорение развития, если
>0
–ускорение развития, если ![]() <0 –замедленное
развитие. Пар-ры ур-я
<0 –замедленное
развитие. Пар-ры ур-я ![]() опред-ся из сис-мы нормальных
ур-ий:
опред-ся из сис-мы нормальных
ур-ий: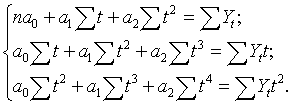
Приняв, что ![]() , то преобразованная сис-ма
нормальных ур-ий будет иметь вид:
, то преобразованная сис-ма
нормальных ур-ий будет иметь вид: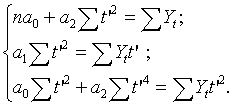
Отсюда ![]()
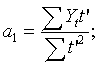 для
нахождения
для
нахождения ![]() и
и ![]() необходимо
решить следующую сис-му нормальных ур-ий:
необходимо
решить следующую сис-му нормальных ур-ий: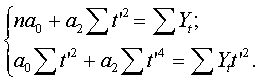
43. Статистическая модель оц-ки развития с переменным ускорением (замедлением).
Такой тип развития опис-ся трендом параболы 3-го порядка:![]()
Если ![]() >0 – эффект ускорения, если
>0 – эффект ускорения, если ![]() <0 – эффект замедления.Для нахождения
пар-ров ур-я тренда параболы 3-го порядка
<0 – эффект замедления.Для нахождения
пар-ров ур-я тренда параболы 3-го порядка ![]() вычислим
из сис-мы нормальных ур-ий:
вычислим
из сис-мы нормальных ур-ий:
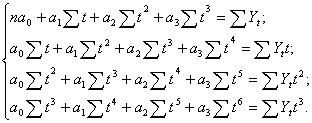
Приняв, что ![]() , получим следующую комбинацию
сис-м нормальных ур-ий для опред-я пар-ров ур-я:
, получим следующую комбинацию
сис-м нормальных ур-ий для опред-я пар-ров ур-я: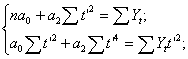
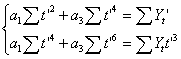
44.Развитие по закону с постоянным темпом роста, т.е. в геометрической прогрессии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.