Этот тип раз-тия описывается уравнением степенной зависимости: 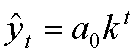 .
.
, где а0 – усредненное значение начальной точки отсчета движения, k в этом уравнении соответствует среднему темпу роста, t – порядковый номер фактора времени.
Если ![]() , то темпы роста возрастают, а при
, то темпы роста возрастают, а при ![]() - снижаются. Для нахождения параметров
уравнения степенной зависимости a0 и k необходимо прологарифмировать исходное уравнения:
- снижаются. Для нахождения параметров
уравнения степенной зависимости a0 и k необходимо прологарифмировать исходное уравнения: ![]() .Параметры логарифмического уравнения lga и lgk определим на основе системы нормальных
уравнений:
.Параметры логарифмического уравнения lga и lgk определим на основе системы нормальных
уравнений:
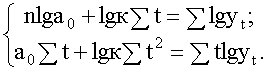
Если ![]() , то значения параметров уравнения
исчислим по формулам:
, то значения параметров уравнения
исчислим по формулам:
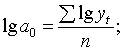
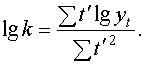
Исходные значения параметров а0 и к получим, взяв антилогарифмы параметров lga0 и lgk.
Рассчитывая теоретические уровни анализируемого динамического ряда при помощи эталонных моделей, можно установить, какому из названных выше типов развития в большей мере соответствует изучаемый процесс. Подобная задача решается на основе определения средней квадратической ошибки аппроксимации, исчисляемой по формуле:
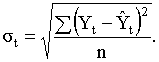
Сравнивая результаты выравнивания, полученные для различных моделей, по
минимальной величине ![]() определяют, какая из
моделей типа развития наиболее подходит для данного динамического ряда.
определяют, какая из
моделей типа развития наиболее подходит для данного динамического ряда.![]()
Кроме того, полученные модели могут быть использованы и в прогностических целях, а их сопоставление за несколько смежных периодов времени (например, за два пятилетия) позволяет выявить смену типов развития, если она имеет место в действительности.
В качестве критерия выбора наилучшего ур-ния тренда может служить коэф-т детерминации. Здесь за основу берется наибольшее значение коэф-та детерминации
45.Стат.методы анализа и прогнозир. сезонных явлений
К сезонным относят такие явления, которые обнаруживают в своем развитии определенные законом-ти, регулярно повторяющиеся через определенные промежутки времени. Статистическое изучение сезонности ставит следующие задачи: 1численно выразить проявление сезонных колебаний, 2выявить их силу, 3вскрыть факторы, вызывающие сезонные колебания, 4выяснить экономические последствия проявления сезонности, осуществить прогноз сезонности. Стат. измерение сезонности осуществляется на основе относит. Показателей, индеков сезонности В статистике используются различные приемы исследования сезонных колебаний. Числовым выражением измерения сезонности являются индексы сезонности. Наиболее доступным способом исчисления индексов сезонности являются результаты сравнения средних, исчисленных по годовым данным для каждого сезонного периода (месяца или квартала), с общей средней, т.е.:
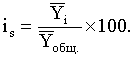
Для определения индексов сезонности широко используется способ скользящих средних. В этом случае фактические уровни (Уi) сравнивается со сглаженными средними:
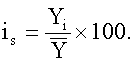
На заключит.этапе рассчитываются общие инд.сезонности по кажд.периоду:
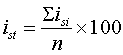
Если индивид.инд.сезонности нанести на график,то получим представлен.о сезонной волне.
Стат.изучение сезонности на основе выравниван(сглаживания)по ур-ням тренда.В этом сл.представляется возможность мультипликативн.или адитивн.модели рассчитать инд-сы сезонности.При этом представл. возможным исходные ур-ни ряда динамики(Yt)по составляющим компонентам:а)влиян.основной тенденции;б)влиян.сезонной компоненты(V(ню)t);в)влияние случайной компоненты(εt)
Применит-но к мультипликат.модели способ действия заключается в
след:1)исходные данные в разрезе сезонных периодов представл-ся во временной
последоват-ти по годам;2)выбир-ся можель ур-ня тренда для выявления
основн.тенднции(![]() );3)получив выравненное
знач.ур-ней по всему ряду g рассчит-ся индивид.индексы сезонности для каждого
квартала:
);3)получив выравненное
знач.ур-ней по всему ряду g рассчит-ся индивид.индексы сезонности для каждого
квартала: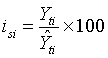 ;4)общие инд.сезонности для кажд.квартала
рассчит-ся:
;4)общие инд.сезонности для кажд.квартала
рассчит-ся: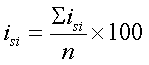 . Проверка правильности расчетов ИС:
. Проверка правильности расчетов ИС: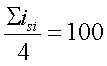 .
.
46. Гармонический анализ рядов с периодическими колебаниями (гармоники Фурье). При исследовании периодических явлений для построения модели сезон-ной волны может быть применен гармонический анализ(ряд Фурье):
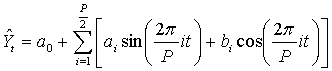
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.