Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 4

Ср. величины предстваляют основу экон. анализа под средством расчета стат. показателей. Сформулируем общий принцип расчета стат. пок-лей в форме ср. величин. Средний уровень признака=итог (объем) признака по сов-сти явлений/численность явлений.

Ср. величина стат. пок-лей рассчитывается также как индивидуальное значение, но только по сов-сти в целом. Рассмотрим алгоритмы, рачеты формулы средних величин:

Средняя арифметическая простая – она применяется в тех случаях, когда значения осредняемого признака представлены в не сгруппированном виде как индивидуальное значение каждой единицы сов-сти. значания осредняемого признака представим: х1,х2, …хn

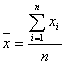 . по сгруппированным данным (по вариационным рядам распределения) значение средней рассчитывется по формуле средней арифметической взвешенной. Имеем ряд распределения. di – удельный вес.

Формула расчета средней арифметической взвешенной имеет вид:

,  

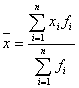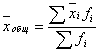
где хi- варианты значений осредняемого признака; fi – частота повторяемости вариантов. При условии, что fi=const средняя арифметическая взвешенная переходит в среднюю арифметическую простую, а именно: , где n – число вариантов. Если в средней арифметической взвешенной частоты выразить удельными весами (долями).

, то расчет арифметической взвешенной примет вид:

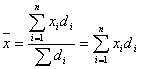. Если удельный вес выражен в % к итогу, то расчет средней арифметической представим формулой вида: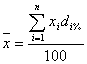. Уровень средней величины зависит как от вариантов значения осредняемого признака (xi), так и от удельного веса (di), единиц сов-сти каждого из вариантов в общем итоге. Расчет средней по удельным весам позволяет определить вклад в формирование среднего уровня каждого подразделения сов-сти по вариантам изучаемого пизнака.

Средняя гармоническая. В тех случая, когда в качестве исходных данных известны варианты  значения осредняемого признака (xi), а также итоги их значений (Mi=xifi), то подобных случаях средняя рассчитывается по формуле средней гармонической взвешенной.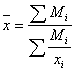. при условии, что Mi=const, то средняя гармоническая взвешенная преобразуется в среднюю гармоническую простую, а именно: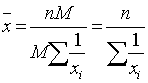. Если вместо абсолютных значений (Mi) взять их удельные веса, то в этих случаях расчет средней гармонической примет вид   

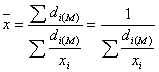
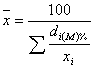. Для исследования стационарных процесс

7.Расчет ср.арифмет.по интерв.вариац.рядам обычн.способом и по способу условн.момента.

Расчет средней по интервальн.вариац.рядам имеет свои особенности.Здесь необх.от интерв.значений признака перейти к дискретным,вычислив полусуммы нижней и верхней границ интервалов: (Хн+Хв)/2.Вычислим среднее значение обычн.способом:Хср.=∑xf/∑f.

Вычислим среднее значение преобразоват.способом(используя величину 1-ого условн. момента).Порядок действий:

1.В рядах распределения с равн.интервалами значение пост.величины А рекоменд.определять так:А=(Хmin+Xmax)/2

2.Вычтем из всех вариантов значений признака пост.величину А.

3.Значения х-А поделим на кратную величину k.В качестве кратной величины k в интерв.рядах с равными интервалами следует брать:

а)величину равного интервала k=i,если в ряду распределения нечетн.число интервалов б)в интерв.вариац.рядах с равн.интервалами в качестве k берется половина интервала k=i/2,если в рядах распределения четн.число интервалов.

4.Вычислить среднюю арифмет.из (х-А)/к,к-рые наз.первым условн.моментом.

m1=∑((x – A)/к)f/∑f

Т.о.расчет средней по интерв.вариац.рядам с равн.интервалами представим: хср.=А+km1

Порядк.№условн.момента зависит от пок-ля степени для значений х-А.На основе с-мы условн.моментов(их комбинаций)рассчитыв.большое число стат.хар-ик.

8.Расчет моды,медианы и квартильных хар-тик.