Выборочный метод в статистике имеет право на существование при условии, если его результаты будут распространены на всю (генеральную) совокупность. Использование выборочного метода приводит к возникновению ошибок в выборке (репрезентативности).
При собственно случайном отборе средняя ошибка выборки при повторном отборе определяется по формуле
,
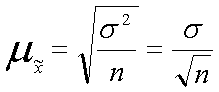Где n – численность выборки;
Ơ2 – дисперсия признака.
В приведенной формуле в качестве Ơ2 берется Ơ2 генеральной совокупности, размер которой нам неизвестен. Поэтому в практических расчетах Ơ2 генеральной совокупности заменяется Ơ2 по выборке.
В мат. стат-ке доказано
Для больших выборок с объемом n>100 различия между значениями 
и 
практически
незначимо.
При бесповторном отборе средняя ошибка выборки
,
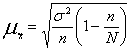С заданной степенью точности (вероятности) определим предельную ошибку выборки
Рассмотрим методику определения ошибки доли. Средняя ошибка доли определяется
1. а) повторный отбор
б) бесповторный отбор
2. С заданным уровнем вероятности p определяем предельную ошибку доли
3. Определяем границы доли по генеральной совокупности
Наряду с абсолютными значениями предельных ошибок
выборки (
и 
)
рассчитывают относит. показатели этих ошибок: а) относит. ошибка средней
определяется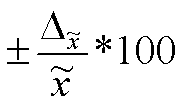 
б) применительно к оценке
относит. доли -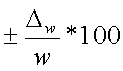 
21.Определ-е ошибок выборки при типическом (районированном) отборе.
Особ-сть типич.выборки заключ-ся в том, что в данном случае генеральная совокуп-ть (ГС) по какому-либо признаку типизации расчлен-ся на качественно однородные (типичные) группы, а затем в пределах каждой производится либо собственно случайный, либо механический отбор.
Виды отбора ед-ц сов-ти из типических групп: 1.пропорциональный отбор (по величине удельного веса в каждой из типических групп), 2.непропорциональный.
Из правила сложения дисперсий известно:
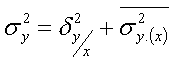
В мат. стат-ке
доказано, что средняя дисперсия равна общей дисперсии: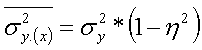 
Известо, что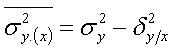 
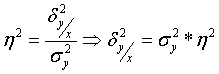
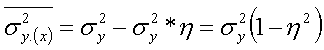
При типическом отборе ошибка выборки всегда <, чем при собств-но случ-ой на вел-ну межгрупп. дисперсии. А именно: пред. ош-ка выборки б-т:
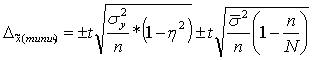, в данной ф-ле n-ч-ло
ед-ц сов-ти, попавших в выборку из всех групп n=n1+n2+…+ni при
пропорциональном способе отбора выборочные х-тики рассчитываются след. обр.
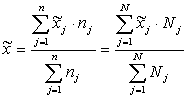
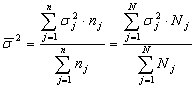
При опред-ии пред. ош-ки доли при типич. сп-бе отбора использ-ся ф-ла:
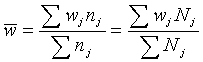
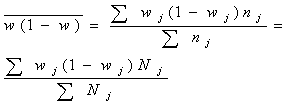
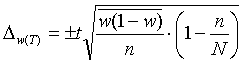- ошибка доли
Границы доли при
типич. отборе: 
Ошибка доли при собсвенно-случ.
Отборе будет иметь вид:
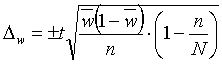
2. при непропорц-м
сп-бе отбора взвешивание производ-ся т-ко по числ-сти групп ГС (
).
В матстат при
непропорц отборе предлагается схема взвешивания по величинам среднеквадратических
отклонений. Числ-ть групп при непропорц отборе рекомендуется определять так: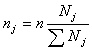 
22. Определение ошибок выборки при серийном отборе.
При серийной выборке отбор производится не единицами, а сериями (гнездами), (как правило серии равновелики) а затем обследуются все ед-цы совок-ти по интересующим нас признакам. Различают равновеликие и разновеликие серии. Предпочтение отдается равновеликим сериям, ибо в этом случае нет необходимости перевзвешивать выборочные характеристики (среднюю и дисперсию).
Методика определения ошибок серийного отбора заключается в следующем. Рассчитывается межсерийная средняя.
Для случая равновеликих серий по формул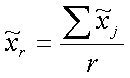е
r -
число серий по выборке
R - число серий в генер. совок-ти.
Для случая равновеликих серий межсерийн. дисперсия расчит.: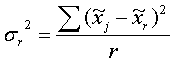 
Предельная ошибка при межсерийном отборе
,
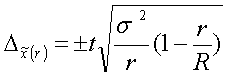
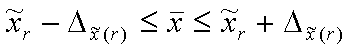Ошибки доли при серийном отборе исчисляются крайне редко.
23. Многоступенчатая (комбинированная) выборка. Моментно-выборочное наблюдение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.