В качестве стандартных показателей, допустим цен на отдельные виды
продуктов и товаров, могут выступать ср. цены, прейскурантные цены,
ср.республиканские цены и т.д. Как прямым способом, так и косвенным,
целесообразно исчислять индексы качественных показателей: цены, себестоимость,
урожайность и т.д. Нецелесообразно строить тер-е индексы объёмных(экстенсивных)
показателей. В тех случаях, когда представляется целесообр-м построение тер-х
индексов объёмных показателей по косвенному методу, то конструкция формул
подобных индексов будет иметь вид: 
:
Полагаем, что подобные тер-е индексы объёмных показателей по касвенному методу можно осуществлять при межзаводских и межрайонных сравнениях. В этих случаях в качестве стандартов объёмных показателей могут выступать (допустим) структура посевов в республиканском масштабе.
Произведение факторных тер-х индексов физического объёма и цен даст тер-й индекс стоимости (выручки) только в том случае, если один из факторных тер-х индексов будет рассчитан по прямому способу, а второй – по косвенному. Проблематика построения тер-х индексов требует дальнейшего теоретического обоснования.
62. Характеристики измерения тесноты связи : лин-й коэф-т корреляции, теоритич-й коэф-т корреляц-го отношения, коэф-т детерминации.
Для измерения тесноты связей используются следующие стат-е коэф-ты:
коэф. кореляц-го отношения(индекс кореляции) и линейный коэф-т корреляции(для
случая измерения тесноты связей для случая лин-х связей). Теснота связей для
нелинейных ур-ний и регрессии исп-ся (примен-ся) корреляционное отношение (либо
индекс корреляции). Известно, что общая дисперсия результативного признака 
=
+
.
; 
; 
.
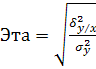В преобразованном виде коэф-т кореляц-го отношения (индекс корреляции
)исчисляется так: R=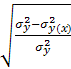
=
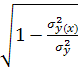, где 
=
.
Для случая линейной парной регрессии для измерения тесноты связей
прим-ся линейный коэф-т корреляции. Он рассчит-ся как ср. арифметич-я из
нормиров-х отклонений результативного и факторного пр-ков, т.е. 
, где 
, 
.
Коэф-т корреляции варьируется в пределе от -1 (обратная зависимость) до
+1 (прямая зависимость). В результате алгеброич-х преобразований получим
формулу исчисления коэф-та корелиции: 
, где 
, 
, 
, 
, 
.
=
.
Линейный коэф-т корреляции можно вычислить по формуле: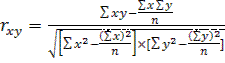 
.
и 
- коэф-ты детерминации. Коэф-т детерминации
показывает долю вариации результативного признака, обусловленную вариацией
факторного признака.
63. Оценка значимости (существенности) коэф-та корреляции (корреляц-го отношения) и коэф-та регрессии.
Для оценки значимости как коэф-та регрессии так и для оценки значимости коэф-та корреляции исп-ся специальные t-критерии.
Оценка значимости(существ-ти) коэф-та регрессии осущ-ся так:
сравнивается 
с 
(
) по таблицам Стьюдента, где n –
число наблюдений; m – число параметров ур-я регрессии, вклячая свободные
члены. И если >, то значимость (существ-ть) влияния на
признак-результат статистически подтверждается, и наоборот.
=
, где 
(при парной зависимости).
Стат. оценка значимости коэф-та корреляции определ-ся таким образом:
если 
существенность тесноты связей между признаками.
, где 
.
67 Непараметрические характеристики тесноты связи. При изучении зависимости между качественными признаками (при отсутствии количественного их измерения) используются различные статистические характеристики (коэффициенты).
Ранговый коэффициент корелляции (коэф-т Спирмана). Здесь кореллируются между собой ранги (порядковые номера показателей. Ранговый коэффициент корелляции Спирмена рассчитывается по формуле:
S=1 – (6∑d2):(n*(n2 – 1)),
где d – разность рангов кореллируемых признаков (результативного и факторного),
n – число наблюдений (изменяется в пределах от -1 до +1).
Если порядковые номера рангов совпадают, то берётся их средняя арифметическая.
Коэффициент корелляции - применяется для измерения тесноты связи при наличии трёх и более признаков. Этот коэф-т исчисляется по формуле:
W=12S:((m2(n3 – 1)),
где m – число признаков (не меньше 3-х);
n – число наблюдений;
S – сумма квадратов отклонений рангов
S=∑(∑Ryxz)2 - (∑Ryxz)2:n
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.