Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 15

Факторная сумма кв.отклонений :

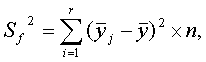 где n –Число набл-й в кажд. Группе,r- число выделяемых групп по факторному признаку, или , где 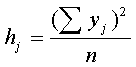; Вычислим сумму кв.отклонений остаточного комплекса:

в) сумма откл-й остат-ого комплекса

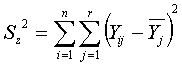         ,      или =-

2.Вычисл. знач-я коэф-ов детерм-ии

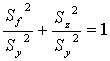,0

3. Опр-ся пок-ли число степ-ей своб.

, в том числе ,

4. Рассчит. дисп-ю на 1 степ. своб.(несмещ-ая оценка дисп-ий)

;

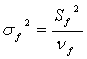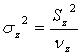
5. Рассчит-ся дисп-ое отн-ие (критерий Фишера)

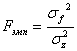, если  и наоборот, т.к. в  числителе расчета  дисперсионного отношения берется наибольшее по абсолютной величине из дисперсий.

6. Сравним  F(эмп) с F(табл) и если F(эмп) > F(табл) то значимость влияния признака-фактора на признак-результат признается стат-ки доказанной. F(табл) находистся по соотв. Таблицам. Входной инфо при определении F(табл) явл. Заданный уровень значимости() и число степеней свободы( и ). В кач-ве  берется число степеней свободы числителя, а в кач-ве - знаменателя

30.Схема двухфакторного дисперсионного анализа.

Для проведения 2ухфакторного ДА необходимо построить комбинационнуб группировку по 2ум факторным признакам, т.е. группы по первому факторному признаку расчленяются на подгруппы по другому признаку. В этом случае модель2ухфакторного ДА представим в след.виде: , где =

Схема решения 2ухфакторного ДА:

1.На первом этапе осущ-ся дисп-ый анал.по схеме 1-факт-ого(оба факт-их приним-ся как один факт-ий комплекс).

2.На 2-ом этапе дается оценка влияния  кажд. из компонентов факторного комплекса.

Сумма кв.отклонений при 2ухфакторном ДА:

 в том числе: 1.=; 2.=;

2.  =-(, где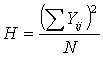

Числа степеней свободы определяются:

;     ;     ;         ()();

Оценка дисперсий  на 1 степ. своб.: ; ;;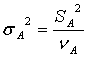

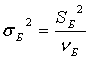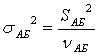Вычислим эмп-ие знач-ия дисп-ых отношений:

Fэмп(А)=  (если); Fэмп(Б)= (если ); Fэмп(АБ)= (если );

=

Эмп-ие знач-ия F-крит. сравн-ся с табл. по кажд. из источн-ов воздействия с заданным Ур-ем знач-сти ()

Дисперс. анализ широко м.б. использован при оценке заначимости (существенности) факторных группировочных признаков. Если Fэмп>Fтабл., то знач-сть этого фактора стат-ски призн-ся существенной.

31.Модель однофактор.ДА при рендомизировании блоков.

Способ построения стат. Исследования, когда предварительно в одном направлении элементы совокупности делятся на блоки соотносительно с выровненными условиями. В этом случае проверяемые  варианты распределяются в случайном порядке, т.е. рендомизируются. Стат. Модель ДА приминительно к поставленной задаче исследования может быть записана в след.виде:

;

-H , где (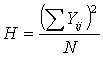)   в том числе:

а) ;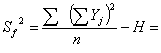

б)

в) ;

Числа степеней свободы: в том числе

; ;

Вычислим показатели оценок дисперсий на одну степ. своб.:

;;

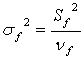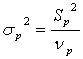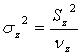
Эмпирическое дисперсионное отношение вычисляется::

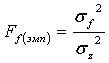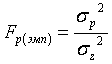 (если); (если )

Эмп. F-критерии сравниваются с табличными: а)приминительно к факторному комплексу( () ).Если Fэмп>Fтабл, то существенность факторного признака доказана.б) приминительно к повторностям ( () ).

32. Аналитические показатели ряда динамики. Взаимосвязь цепных и базисных темпов роста.

Исходным показателем динамического ряда является его уровень, показывающий, на каком уровне протекает развитие. Изменение уровней динамики характеризуется системой показателей (аналитических, расчетных):

абсолютный прирост, темп роста, темп прироста и абсолютный размер 1% прироста. Эти показатели могут быть подсчитаны по двум принципам – цепному и базисному.

Абсолютный прирост – это разность между данным и уровнем принятым за базу. Абсолютные приросты цепным способом рассчитываются как разность между каждым последующим (У_i) и предыдущим (у_i-1) уровнями ряда динамики, то есть у_i-y_i-1.

Абсолютные приросты базисным способом исчисляются как разность между каждым последующим уровнем ряда (Y_i) и начальным (Y₁), то есть Y_i-Y₁. Абсолютный прирост показывает, на сколько данный уровень ряда превышает уровень, взятый для сравнения. Абсолютный прирост может быть положительным и отрицательным.