Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 11

х(средняя)=Ме=Мо

Ур-ние нормального распределения (колокол Гауса) выражается ф-цией: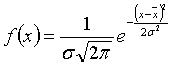  

Для построения кривой нормального распределения надо знать  два параметра х(среднее) и σ.

Для удобства вычислений вероятностей случайных величин (х_i) нормируются , а затем используются ранее рассчитанные (табулированные) значения плотности ф-ции з-на нормального распределения.

Нормированные значения определяются .

Ф-ция з-на нормального распределения в стандартизированном масштабе примет вид:

 .

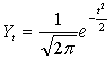Отметим, что значение нормированных переменных: укладывается в пределы +-3 σ. Особенности кривой нормального распределения: 1. кривая симметрична относительно оси ординат. В этом случае максимальная ордината = значению х(средняя)=Ме=Мо. Величина ординаты равна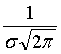.2. кривая симметрически приближается к оси абсцисс. Приближаясь по обе стороны до бесконечности, т.е. чем больше заначение признака лтклоняется от х (средней), тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку отклонения значения х_i от х (среднего) равновероятны.3 (ГРАФИК)

иосительно кривой ординатого распределения: первая кривая а параметра ом, можно ли отнести данное эмпирич. вестна.

Кривая имеет две точки перегиба, находящихся на расстоянии +- σ. При отклонеии значении признака от средней на +- σ при t=1, р=0,683. вероятность того, что отклонение значения признака будет на +-2 σ при t =2, р=0,924, вероятность того, что отклонение значения признака будет укладываться в +-3 σ при t =3, р=0,997. 4. при х=const с увеличением значения σ кривая становиться более пологой, при σ=const с изменением х (среднего) кривая принимает свою форму. В мат. стат-ке разработана концепция точности распределения вер-стей по формуле интеграла Лапласса применительно к з-ну нормального распреления. Формула интеграла Лапласа имеет вид 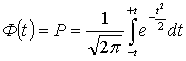. На основании этой формулы разработаны таблицы плотности распределения вероятности. Для выравнивания частот эмпирического ряда (нахождение теоритичесикх частот) необходимо рассчитать вер-сти попадания частот в тот или иной интервал ряда распределения. В данном случае необходимо рассчитать теоритичесике (выровненные) значения частот интервально ряда. Для этого необходимо . Исходным основанием для расчета вероятностей является следующее выражение . При выравнивании частот эмпирического ряда в исходную таблицу внесены дополнительные реквизиты. Процедура вычисления вер-сти состоит в след.: определяются нормированные значения нижних границ и нормированные значения верхних границ интервалов . По значениям нормированных величин находят половинные значения вер-стей.

19. Критерии согласия Хи-квадрат К.Пирсона и λ академика А. Колмогорова

Для оценки соответствия эмпирического распределения теоритическому  используется критерий согласия λ-академика Колмогорова, Χ² К. Пирсона.

, гдеD_n- максимальная разность накопленных частот (эмпирических и теоритическиъ), т.е. между D_nи λсуществует след. соотношение . Если D_{n(эмпир)}> D_n(табл),  тосделать заключение о соответствии эмпирического распределения теоритическому нельзя и наоборот.

Критерий Карла Пирсона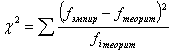. Здесь сравнивают Χ²(эмпирич) с Χ² (теорит). Χ²(эмпирич)> Χ² (_{ά ν)}(табл). О характере соответствия речь не идет и наоборот. Χ² (табл.) определяется с заданным ур-нем значимости α  и ν – число степеней свободы. Применительно к  выравниванию частот по з-ну нормального распределения: ν=n-3, где n – число групп ряда распределения, 3 – число параметров в ур-нии нормального распределения.

20. Определение ошибок выборки при собственно случайном отборе (предельные ошибки средней и доли)

Математ. теория выборочного наблюдения разработана к собственно случайной выборке. Особенность этого способа отбора состоит в соблюдении принципа случайности. В данном случае отбор производится либо по жребию, либо по таблице случайных чисел.