Краткие ответы на вопросы № 1-71 по курсу "Статистика" (Определение статистики как науки. Методы контроля за полнотой и достоверностью данных стат наблюдения), страница 22

49,50. Особенности моделир-ния рядов динамики с пом-ю корреляционно-регрессионн. анализа. Автокоррел.и авторегр.

При корреляционно-регрессионном анализе классические методы мате-матической статистики применимы при условии,  если отдельные члены стати-стического ряда независимы в смысле теории вероятностей (являются случай-но независимыми).

Особенности: Каждый последующий ур-нь ряда зависит от предыдущего,т. е.сказывается наличие автокорреляции.

Корреляц-регр.анализ строится на предпосылке независ-ти(случайности)ур-ней стат.совокупности. При корреляц.ур-ней временных рядов необходимо устранить автокорреляцию(привести исходный ряд динамики к стандартному виду). Наличие(отсутствие)автокоррел.в исходных ур-нях ряда динамики проверяется на основе коэфф-та автокоррел. Для расчета коэфф.автокоррел. по каждой переменной необходимо привести исходные ур-ни ряда динамики и эти же ур-ни ряда динамики со сдвигом на 1 ур-нь вниз.По этим данным рассчит-ся обычный коэфф.корреляц.Его называют первым нециклическим коэфф. автокоррел.().Эмпирич-й коэфф. автокорр. 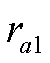сравнивают с табличным с ур-м значимости 5% или 1%.Для нахождения табл.значения автокорр.берется число наблюдений-1.(V(ню)=N-1).Если эмп>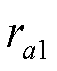табл, то наличие автокорр.подтверждается,и наоборот.

Устранение автокорр. производится различн.способами:1)рассчит-ся первые разности(цепные и абсолютные приросты)по исходным переменным:

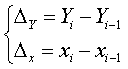
2)Коррелир-ние отклонений ур-ней ряда от ур-ней тренда(коррелир-е остатков):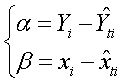

3)Для приведения ряда динамики к стационарному виду рекомендуется в ур-нии регрессии в кач-ве независ. переменной ввести порядков.номер фактора времени ti,т.е.:

В эконометрике дается обоснование возможности коррелир-я самих исходных ур-ней(без их приведения к стационарному виду,при условии,если как по результат-му,так и по факторным признакам обозначена тенденция(тренд) однопланового направления).Этот принцип регресс. анализа наз-ся ко-интеграцией. Для оценки ко-интеграции сущ.специальный критерий.

51 Способы устранен.автокоррел. Проверка гипотезы об отсутствии(наличии) автокоррел.в остаточных величинах (критерий Дарвина-Уотсона).

Для проверки наличия автокорреляции в остатках используется коэфф-ент Дарвина-Уотсона.Между коэфф-том автокорр.для остаточных величин и критерием Дарвина сущ-ет след.взаимосвязь:d=2(1-r_а). Табл.оценки автокорр.и значение критер.Дарвина:

Для более полного и точного суждения о возможности принятия(непринятия) гипотезы об автокорр.в остаточных величинах для разного числа наблюден.и независимых переменных в ур-нях регрессии опред-ются верхние  и нижн.критич.границы.Для проверки гип-зы об отсутствии автокорр.в остаточных величинах эмпирич.значения V(ню)сравниваются с и.Здесь возможны такие варианты:1)если >,то гип-за об отсутств.автокорр.принимается; 2)если <,то отвергается; 3)если≤d≤, то ничего определенного.

52. Оценка тесноты связи на основе пок-лей рядов динамики.

При изучении зависимости между качеств. признаками (при отсутствии их колич-ого выражения) используются разл. стат. хар-ки (коэф-ты):

1. Ранговый коэф-нт корреляции (коэф-нт Спирмена): здесь коррелируются между собой ранги, порядковые номера пок-лей. Ранговый коэф-нт корреляции Спирмена рассчитывается:

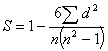, где d- разность рангов коррелируемых признаков (рез-ого и факторного)

n- число наблюдений (-1<n<1)