Определение и примеры метрических пространств

Глава II

Метрические пространства

§8. Определение и примеры метрических пространств

Одной из важнейших операций анализа является операция предельного перехода. В основе этой операции лежит тот факт, что для точек числовой прямой определено расстояние от одной точки до другой. Ряд фундаментальных фактов анализа не связан с алгебраической природой множества действительных чисел (т. е. с тем, что для них определены операции сложения и умножения, подчиненные известным правилам), а опирается лишь на те свойства действительных чисел, которые связаны с понятием расстояния. Это обстоятельство естественно приводит к понятию «метрического пространства», играющему фундаментальную роль в современной математике. Ниже будут изложены основные факты теории метрических пространств. Результаты этой главы будут играть существенную роль во всем дальнейшем изложении.

Определение. Метрическим пространством называется совокупность некоторого множества X элементов, называемых точками, и расстояния, т. е. однозначной, неотрицательной действительной функции  определенной для любых х и у из X и удовлетворяющей следующим условиям:

1)  тогда и только тогда, когда х = у,

2) (аксиома симметрии)

3) (аксиома треугольника)

Само метрическое пространство, т. е. совокупность X и  мы будем обозначать обычно

В случаях, когда это не может привести к недоразумениям, мы будем иногда обозначать метрическое пространство тем же символом, что и сам «запас точек» X.

Приведем ряд примеров метрических пространств. Некоторые из указанных ниже пространств играют в анализе весьма важную роль.

1. Положив для элементов произвольного множества

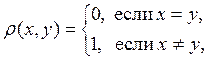
мы получим, очевидно, метрическое пространство.

2. Множество D¹действительных чисел с расстоянием

образует метрическое пространство R¹.

3. Множество Dⁿупорядоченных групп из п действительных чисел

с расстоянием

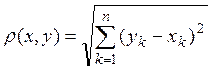
называется n-мерным координатным евклидовым пространством  Справедливость аксиом 1 и 2 для  очевидна. Для доказательства того, что аксиома треугольника также выполнена в  воспользуемся неравенством Коши-Буняковского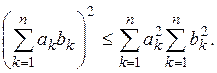[1]:

                                                  (1)

Если

то, положив

получим

в силу неравенства Коши-Буняковского

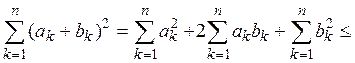
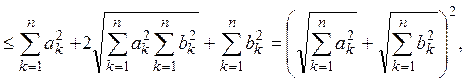т.е.

или

4. Рассмотрим пространство  в котором точками являются опять-таки системы п чисел  а расстояние определяется формулой

Справедливость аксиом 1-3 очевидна. Это пространство во многих вопросах анализа не менее удобно, чем евклидово пространство

Примеры 3 и 4 показывают, что иногда действительно важно иметь различные обозначения для множества точек метрического пространства и для самого метрического пространства, так как один и тот же запас точек может быть различным образом метризован.

5. Множество  всех непрерывных действительных функций, определенных на сегменте [a, b] с расстоянием

(2)

также образует метрическое пространство. Аксиомы 1-3 проверяются непосредственно. Это пространство играет очень важную роль в анализе. Мы будем его обозначать тем же символом  что и само множество точек этого пространства. Пространство непрерывных функций на сегменте [0, 1] с указанной выше метрикой мы обозначим просто С.

6. Обозначим l₂метрическое пространство, в котором точками являются всевозможные последовательности

действительных чисел, удовлетворяющие условию

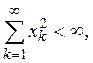
а расстояние определяется формулой

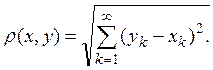                                                   (3)

Докажем прежде всего, что так определенная функция  всегда имеет смысл, т.е. что ряд 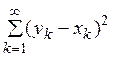 сходится. Для любого натурального п имеем (см. пример 3):

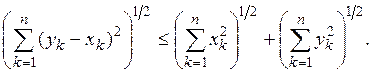                                 (4_n)

Пусть теперь  По условию правая часть этого неравенства имеет предел. Таким образом, выражение, стоящее слева, при  не убывает и ограничено; следовательно, оно стремится к пределу, т.е. формула (3) имеет смысл. Заменив в (4_n) х на –х и перейдя к пределу при  получим

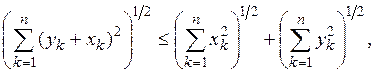                            (4)

а это по существу уже и есть аксиома треугольника. Действительно, пусть

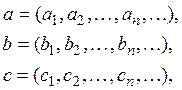
три точки из l₂. Положим,

тогда

и в силу (4)

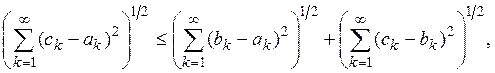
т.е.

7. Рассмотрим, как и в примере 5, совокупность всех непрерывных функций на отрезке [а, b], но расстояние определим иначе, а именно положим

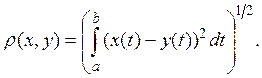                                        (5)

Такое метрическое пространство мы будем обозначать  и называть пространством непрерывных функций с квадратичной метрикой. Здесь аксиомы 1 и 2 определения метрического пространства опять-таки очевидны, а аксиома треугольника непосредственно вытекает из интегральной формы неравенства Коши-Буняковского

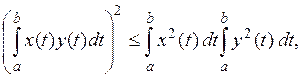
которая может быть получена, например, из легко проверяемого тождества

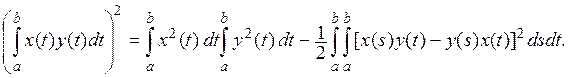
8. Рассмотрим множество всех ограниченных последовательностей  действительных чисел. Положив

                                               (6)

мы получим метрическое пространство  Справедливость аксиом 1-3 очевидна.

9. Неограниченное количество дальнейших примеров доставляет следующий принцип: если