Определение и примеры метрических пространств, страница 19

Достаточность. Так как М компактно, то из всякой последовательности  можно выбрать подпоследовательность, сходящуюся к некоторому  Если М замкнуто, то  т. е. М компактно в себе.

Отсюда и из теоремы 1 § 16 вытекает

Следствие. Всякое замкнутое ограниченное подмножество евклидова пространства является компактом.

Теорема 2. Для того чтобы метрическое пространства было компактом, необходимо и достаточно, чтобы оно было: 1) полно, 2) вполне ограничено.

Доказательство этой теоремы представляет собой дословное повторение доказательства теоремы 1 § 16.

Теорема 3. Всякий компакт К содержит конечное или счетное всюду плотное множество.

Доказательство. Так как компакт является вполне ограниченным пространством, то для каждого п в К найдется конечная -сеть:  Объединение всех этих -сетей представляет собой конечное или счетное множество. Отсюда и из теоремы 4 § 10 вытекает

Следствие. Всякий компакт имеет счетный базис.

Теорема 4. Для того чтобы метрическое пространство R было компактом, необходимо и достаточно каждое из двух условий:

1) Любое открытое покрытие  пространства R содержит конечное подпокрытие.

2) Любая центрированная[9] система  замкнутых множеств в R имеет непустое пересечение.

Доказательство. Заметим, прежде всего, что эквивалентность сформулированных двух условий непосредственно вытекает из принципа двойственности (§ 1). Действительно, если  — открытое покрытие пространства R, то  — система замкнутых множеств, удовлетворяющая условию

                                                          (1)

Условие, что из  можно выбрать конечное подпокрытие, равносильно тому, что система замкнутых множеств  не может быть центрированной, если она имеет пустое пересечение.

Докажем теперь, что условие 1 необходимо и достаточно для того, чтобы R было компактом.

Необходимость. Пусть R — компакт и  — его открытое покрытие. Выберем в R для каждого  конечную -сеть, состоящую из точек  и окружим каждую из этих точек сферой  радиуса  Ясно, что при любом п

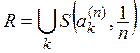                                                          (2)

Предположим, что из  нельзя выбрать конечной системы множеств, покрывающих R. Тогда при каждом п найдется по крайней мере одна сфера  которая не может быть покрыта конечным числом множеств  Выберем для каждого п такую сферу и рассмотрим последовательность их центров  Так как R — компакт, то существует точка  предельная для этой последовательности. Пусть  — множество из  содержащее  Так как  открыто, то найдется такое  что  Выберем теперь номер п и точку  так, чтобы  Тогда, очевидно,  т.е. сфера  покрывается даже одним множеством  Полученное противоречие доказывает наше утверждение.

Достаточность. Допустим, что пространство R таково, что из всякого его открытого покрытия можно выбрать конечное подпокрытие. Докажем, что R — компакт. Для этого достаточно доказать что R полно и вполне ограничено. Пусть  Взяв вокруг каждой точки  окрестность  получим открытое покрытие R. Выберем из этого покрытия конечное подпокрытие  Ясно, что центры этих окрестностей  образуют в R конечную -сеть. Так как  произвольно, то R вполне ограничено. Пусть теперь  — последовательность вложенных друг в друга замкнутых сфер, радиусы которых стремятся к нулю. Если их пересечение пусто, то множества  образуют открытое покрытие R, из которого нельзя выбрать конечного подпокрытия. Таким образом, из условия 1 следует полнота и полная ограниченность, т. е. компактность R.

Теорема 5. Непрерывный образ компакта есть компакт.

Доказательство. Пусть X — компакт и  — его непрерывный образ. Пусть, далее,  — открытое покрытие пространства Y. Положим  Так как при непрерывном отображении прообраз открытого множества открыт, то  — открытое покрытие пространства X. Так как X — компакт, то из покрытия  можно выбрать конечное подпокрытие  Тогда соответствующие множества  образуют конечное подпокрытие покрытия