Определение и примеры метрических пространств, страница 10

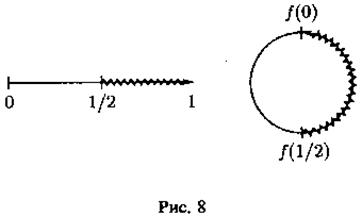
Замечание. Образ замкнутого множества при непрерывном отображении не обязательно замкнут, как показывает следующий пример: отобразим полуинтервал [0, 1) на окружность той же длины.

Множество [ 1), замкнутое в [0, 1), переходит при этом отображении в незамкнутое множество.

Так как в случае отображения «на» прообраз дополнения равен дополнению прообраза, то справедлива следующая теорема, двойственная теореме 2.

Теорема 2'. Для того чтобы отображение f пространства R на R' было непрерывно, необходимо и достаточно, чтобы прообраз каждого открытого множества из R' был открыт.

Для непрерывных отображений справедлива следующая теорема, аналогичная хорошо известной из анализа теореме о непрерывности сложной функции.

Теорема 3. Если R, R', R" — метрические пространства, а f и  — непрерывные отображения R в R' и R' в R". соответственно, то отображение  пространства R в R" непрерывно.

Доказательство проводится: в точности так же, как и для числовых функций.

Отображение f называется гомеоморфным, если оно взаимно однозначно и взаимно непрерывно (т. е. непрерывно как f, так и обратное отображение ).

Пространства R и R' называются гомеоморфными, если между ними можно установить гомеоморфное соответствие.

Легко видеть, что любые два интервала гомеоморфны, что любой интервал гомеоморфен R₁и т. д.

Из теоремы, доказанной в этом параграфе, следует, что: для того чтобы взаимно однозначное отображение было гомеоморфным, необходимо и достаточно, чтобы замкнутые (открытые) множества соответствовали замкнутым (открытым).

Отсюда следует, что: для того чтобы взаимно однозначное отображение  было гомеоморфным, необходимо и достаточно, чтобы для любого М имело место равенство

(Это следует из того, что [М] есть пересечение всех замкнутых множеств, содержащих М, т. е. минимальное замкнутое множество, содержащее М.)

Пример. Рассмотрим пространства  и  (см. §8, примеры 3 и 4). Для отображения, ставящего в соответствие элементу из R с координатами  элемент из  с теми же координатами, имеет место следующее неравенство:

и, следовательно, в любой  - окрестности точки х пространства  содержится некоторая  - окрестность этой же точки х, рассматриваемой как элемент пространства  и наоборот. Отсюда вытекает, что наше отображение  на  есть гомеоморфизм.

Важным частным случаем гомеоморфизма является изометрическое отображение.

Говорят, что взаимно однозначное отображение  метрического пространства R на метрическое пространство R' является изометрическим, если

для любых  Сами пространства R в R', между которыми можно установить изометрическое соответствие, называются изометричными между собой.

Изометрия двух пространств R и R' означает, что метрические соотношения между их элементами одни и те же, а различна, может быть лишь природа их элементов, что несущественно. В дальнейшем два изометрических между собой пространства мы будем рассматривать просто как тождественные.

(1) Понятие непрерывности отображения может быть определено не только Для метрических, но и для любых топологических пространств; именно, отображение f топологического пространства Т в топологическое пространство Т' называется непрерывным в точке  если для любой окрестности  точки  найдется такая окрестность  точки  что

Теоремы 2 и 3 автоматически переносятся на непрерывные отображения топологических пространств.

§ 13. Полные метрические пространства

С первых шагов изучения математического анализа мы убеждаемся в том, какую важную роль в анализе играет свойство полноты числовой прямой, т.е. тот факт, что всякая фундаментальная последовательность действительных чисел сходится к некоторому пределу. Числовая прямая представляет собой простейший пример так называемых полных метрических пространств, основные свойства которых мы рассмотрим в этом параграфе.

Будем называть последовательность  точек метрического пространства R фундаментальной, если она удовлетворяет критерию Коши, т. е. если для любого  существует такое число  что  для всех