Определение и примеры метрических пространств, страница 20

Теорема 6. Взаимно однозначное и непрерывное в одну сторону отображение компакта на компакт есть гомеоморфизм.

Доказательство. Пусть  — взаимно однозначное и непрерывное отображение компакта X на компакт Y. Так как, согласно предыдущей теореме, непрерывный образ компакта есть компакт, то для любого замкнутого  множество  есть компакт, следовательно,  замкнуто в Y. Мы получим, что прообраз, при отображении  любого замкнутого множества  замкнут, т.е. отображение  непрерывно.

Замечание. Из теоремы 6 вытекает следующий результат: если уравнение

                                                          (3)

где функция f(x, у)непрерывна в некоторой замкнутой ограниченной области G, содержащей точку  при каждом  принадлежащем некоторому отрезку [а, b], имеет единственное решение, удовлетворяющее начальному условию  то это решение непрерывно зависит от начального значения

Действительно, так как функция f(x, у) непрерывна в замкнутой ограниченной области, то она ограничена, следовательно, совокупность Р решений уравнения (3), отвечающих начальным значениям, принадлежащим отрезку [а, b], равномерно ограничена и равностепенно непрерывна. Кроме того, множество Р замкнуто. Действительно, если  — последовательность решений уравнения (3), равномерно сходящаяся к некоторой функции  то  есть также решение уравнения (3), так как если

то, переходя к пределу при  получаем

При этом

В силу теоремы Арцела и теоремы 1 этого параграфа отсюда следует, что Р — компакт.

Поставим в соответствие каждому решению  уравнения (3) точку  отрезка [а, b]. По условию это соответствие взаимно однозначно. Кроме того, так как

то отображение  непрерывно. В силу теоремы 6 обратное отображение также непрерывно, а это и означает непрерывную зависимость решений от начальных условий.

Пусть теперь  — множество всех непрерывных отображений y = f(x) компакта X в компакт Y. Введем в  расстояние при помощи формулы

Легко проверить, что таким образом  превращается в метрическое пространство.

Отображение у = f(x) мы назовем равномерно непрерывным, если для любого  найдется такое  что  Для всех  таких, что  Справедливо следующее утверждение: «Всякое непрерывное отображение компакта в компакт равномерно непрерывно», которое доказывается тем же методом, что и равномерная непрерывность функции, непрерывной на отрезке.

Теорема 7 (Обобщенная теорема Арцела). Для компактности множества  необходимо и достаточно, чтобы входящие в D функции y = f(x) были равностепенно непрерывны, т. е. чтобы для любого  существовало такое  что из

                                                      (1)

вытекает

                                                 (2)

каковы бы ни были f из D и х' и х" из X.

Докажем сначала необходимость. Если D компактно, то в D существует конечная -сеть  Так как каждое из отображений  непрерывно, то оно равномерно непрерывно, поэтому найдется такое  что

как только

Тогда

как только  а это и означает, что отображения равностепенно непрерывны.

Докажем теперь достаточность. Погрузим  в пространство  всех отображений компакта X в компакт Y, с той же самой метрикой

которая была введена в  и докажем компактность множества D в  Так как  замкнуто в [10] то из компактности множества D в  следует его компактность в

Зададим  произвольно и выберем  так, чтобы из (1) вытекало (2) для всех f из D и всех x', x" из X. Пусть точки  образуют -сеть в X. Легко видеть, что X можно представить как сумму непересекающихся множеств  таких, что из  следует, что  Действительно, достаточно положить, например,

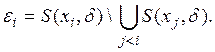
Рассмотрим теперь некоторую конечную -сеть  в компакте Y, обозначим через L совокупность функций g(х), принимающих на множествах  значения  Число таких функций, очевидно, конечно. Покажем, что они образуют -сеть по отношению к D в  Действительно, пусть  Для всякой точки  из  найдется такая точка  из  что