Определение и примеры метрических пространств, страница 7

(1) Пусть  — множество всех функций f из  удовлетворяющих так называемому условию Липшица

где К — некоторое фиксированное число. Множество  замкнуто. Оно совпадает с замыканием множества всех дифференцируемых функций таких, что

(2) Множество  всех функций, каждая из которых удовлетворяет условию Липшица при каком-либо К, не замкнуто. Так как М содержит множество всех многочленов, то его замыкание есть все пространство

(3) Пусть в одном и том же множестве X расстояние определено двумя различными способами, т.е. заданы две различные метрики  и  Метрики  и  называются эквивалентными, если существуют два таких постоянных положительных числа а и b, что 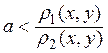 для всех  из R. Если некоторое множество  замкнуто (открыто) в смысле метрики  то оно замкнуто (открыто) и в смысле любой метрики  эквивалентной

(4) Ряд важных определений и утверждений, относящихся к метрическим пространствам (например, определение связности), использует не само понятие метрики, а только понятие открытого (замкнутого) множества, или, что по существу то же самое, понятие окрестности. В частности, во многих вопросах метрику, введенную в том или ином метрическом пространстве, можно заменить любой другой метрикой, эквивалентной первоначальной. Эта точка зрения, естественно, приводит к понятию топологического пространства, являющемуся обобщением понятия метрического пространства.

Топологическим пространством называется множество Т элементов произвольной природы (называемых точками этого пространства), некоторые подмножества которого объявлены открытыми множествами. При этом предполагается, что выполнены следующие аксиомы:

1°. Все Т и пустое множество открыты.

2°. Сумма любого (конечного или бесконечного) числа и пересечение любого конечного числа открытых множеств открыты.

Множества T \ G, дополнительные к открытым, называются замкнутыми. Из аксиом 1° и 2° следует, что:

1'. Пустое множество и все Т замкнуты.

2''. Пересечение любого (конечного или бесконечного) числа и сумма любого конечного числа замкнутых множеств замкнуты. Окрестностью точки  назовем любое открытое множество, содержащее х.

Естественным образом вводятся понятия точки прикосновения, предельной точки, замыкания, а именно:  называется точкой прикосновения множества М, если каждая окрестность точки х содержит хотя бы одну точку из М; х называется предельной точкой множества М, если каждая окрестность точки х содержит бесконечно много точек из М. Совокупность всех точек прикосновения множества М называется замыканием [М]множества М.

Легко показать, что замкнутые множества (определенные нами как дополнения открытых), и только они, удовлетворяют условию [М] = М. Как и в случае метрического пространства, [М] есть наименьшее замкнутое множество, содержащее M.

Так же, как метрическое пространство есть совокупность множества точек и метрики, топологическое пространство есть совокупность множества точек и топологии, определенной в этом пространстве. Ввести в Т топологию — значит указать в нем те подмножества, которые считаются открытыми в Т.

Примеры. (4-а) В силу теоремы 1' открытые множества в метрическом пространстве удовлетворяют условиям 1° и 2° определения топологического пространства. Таким образом, всякое метрическое пространство можно рассматривать как топологическое пространство.

(4-б) Пусть Т состоит из двух точек а и b, причем открытыми множествами являются все Т, пустое множество и множество, состоящее из одной точки b. Аксиомы 1° и 2° выполнены. Замкнутые множества: все Т, пустое множество и множество, состоящее из одной точки а. Замыкание множества, состоящего из точки b, есть все Т.

(5) Топологическое пространство Т называется метризуемым, если в множестве Т можно ввести метрику так, чтобы множества, открытые в смысле этой метрики, совпадали с открытыми множествами исходного топологического пространства. Пространство (4-6) представляет собой пример топологического пространства, которое не может быть метризовано.