Определение и примеры метрических пространств, страница 5

§ 10. Открытые и замкнутые множества

В этом параграфе мы рассмотрим важнейшие типы множеств в метрическом пространстве, а именно открытые и замкнутые множества.

Множество М, лежащее в некотором метрическом пространстве R, называется замкнутым, если оно совпадает со своим замыканием: [М] = М. Иначе говоря, множество называется замкнутым, если оно содержит все свои предельные точки.

В силу теоремы 1 § 9 замыкание любого множества М есть замкнутое множество. Из теоремы 2 § 9 вытекает, что [М] есть наименьшее замкнутое множество, содержащее М.

Примеры. 1. Любой сегмент [а, b] числовой прямой есть замкнутое множество.

2. Замкнутая сфера представляет собой замкнутое множество. В частности, в пространстве  множество функций f, удовлетворяющих условию  замкнуто.

3. Множество функций, удовлетворяющих условию  (открытая сфера), не замкнуто; его замыкание есть совокупность функций, удовлетворяющих условию

4. Каково бы ни было метрическое пространство R, пустое множество и все R суть замкнутые множества.

5. Всякое множество, состоящее из конечного числа точек, замкнуто.

Основные свойства замкнутых множеств можно сформулировать в виде следующей теоремы:

Теорема 1. Пересечение любого числа и сумма любого конечного числа замкнутых множеств суть замкнутые множества.

Доказательство. Пусть  где  — замкнутые множества.

Пусть, далее, х — предельная точка множества F. Это означает, что любая ее окрестность  содержит бесконечно много точек из F. Но тогда тем более  содержит бесконечно много точек из каждого  и, следовательно, так как все  замкнуты, точка х принадлежит каждому  таким образом,  т. е.  замкнуто.

Пусть теперь F — сумма конечного числа замкнутых множеств: 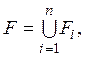 и пусть точка х не принадлежит F, Покажем, что х не может быть t=i

предельной для F. Действительно, х не принадлежит ни одному из замкнутых множеств  следовательно, не является предельной ни для одного из них. Поэтому для каждого i у точки х можно найти окрестность  содержащую не более чем конечное число точек из  Взяв из окрестностей  наименьшую, мы получим окрестность  точки х, содержащую не более чем конечное число точек из F.

Итак, если точка х не принадлежит F, то она не может быть предельной для F, т. е. F замкнуто. Теорема доказана.

Точка х называется внутренней точкой множества М, если существует окрестность  этой точки, целиком содержащаяся в М.

Множество, все точки которого — внутренние, называется открытым множеством.

Примеры. 6. Интервал (а, b) числовой прямой D¹есть открытое множество; действительно, если  то  где  целиком содержится в интервале (а, b).

7. Открытая сфера S(a, r) в любом метрическом пространстве R есть открытое множество. Действительно, если  то  Положим  Тогда

8. Множество непрерывных функций, удовлетворяющих условию  где К — некоторое число, представляет собой открытое подмножество пространства

Теорема 2. Для того чтобы множество М было открыто, необходимо и достаточно, чтобы его дополнение  Р \ М до всего пространства R было замкнуто.

Доказательство. Если М открыто, то каждая точка  имеет окрестность, целиком принадлежащую М, т. е. не имеющую ни одной общей точки с R \ М. Таким образом, ни одна из точек, не принадлежащих R \ М, не может быть точкой прикосновения для R \ М, т. е. R\ M замкнуто. Обратно, если R\ М замкнуто, то любая точка из М имеет окрестность, целиком лежащую в М, т. е. М открыто.

Так как пустое множество и все R замкнуты и в то же время являются дополнениями друг для друга, то из доказанной теоремы вытекает

Следствие. Пустое множество и все R открыты.

Из теоремы 1 и из установленного в § 1 принципа двойственности (пересечение дополнений равно дополнению суммы, сумма дополнений равна дополнению пересечения) вытекает следующая важная теорема, двойственная теореме 1.

Теорема 1'. Сумма любого числа и пересечение любого конечного числа открытых множеств суть открытые множества.