Определение и примеры метрических пространств, страница 17

Выберем теперь из последовательностей

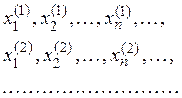
«диагональную» подпоследовательность

эта подпоследовательность фундаментальна, так как все ее члены, начиная с лежат внутри сферы радиуса  Так как пространство R полно, то эта подпоследовательность имеет предел.

Доказательство теоремы закончено.

Часто бывает полезно следующее обобщение теоремы 1.

Теорема 2. Для того чтобы множество М, лежащее в полном метрическом пространстве R, было компактно, необходимо и достаточно, чтобы при всяком  для М существовала в R компактная -сеть.

Доказательство. Необходимость тривиальна, докажем достаточность. Пусть  задано и пусть А — компактная -сеть для М. Выберем в А конечную -сеть. Ясно, что она будет представлять собой конечную -сеть для М; следовательно, в силу предыдущей теоремы, множество М компактно.

§ 17. Теорема Арцела и ее применения

Применение теорем 1 и 2 предыдущего параграфа, дающих необходимые и достаточные условия компактности, к отдельным частным случаям не всегда просто. Для множеств, расположенных в том или ином специальном пространстве, могут быть даны специальные критерии компактности, более удобные для практического использования.

В анализе одним из важнейших метрических пространств является пространство

Для подмножеств этого пространства наиболее важный и часто используемый критерий компактности доставляет так называемая теорема Арцела.

Для того чтобы ее сформулировать, нам необходима сперва ввести следующие понятия.

Семейство  функций, определенных на некоторою отрезке, называется равномерно ограниченным, если существует такое число М, что

для всех х и для всех  принадлежащих данному семейству.

Семейство функций называется равностепенно непрерывным, если для каждого  найдется такое  что

для всех  таких, что  и для всех  из данного семейства.

Теорема Арцела. Для того чтобы семейство непрерывных функций, определенных на отрезке [а, b], было компактно в  необходимо и достаточно, чтобы это семейство было равномерно ограничено и равностепенно непрерывно.

Доказательство. Необходимость. Пусть множество Ф компактно в  Тогда, по теореме 1 § 16, в Ф существует для каждого положительного  конечная -сеть  Каждая из функций  как непрерывная функция на отрезке, ограничена:

Положим  По определению -сети для всякого  имеем хотя бы для одного

Следовательно,

Итак, Ф равномерно ограничено.

Далее, так как каждая из функций  образующих -сеть, непрерывна, а следовательно, и равномерно непрерывна на [а, b], то для данного  существует такое  что

если

Положим  Тогда при  для любой функции  выбрав  так, что  имеем:

       

Равностепенная непрерывность Ф также доказана.

Достаточность. Пусть Ф — равномерно ограниченное и равностепенно непрерывное семейство функций. Согласно теореме 1 § 16, для того чтобы доказать его компактность в  достаточно показать, что при любом  для него в  существует конечная -сеть. Пусть

и пусть  выбрано так, что

для всех  Разобьем отрезок [а, b] на оси х точками  на интервалы длины меньше  и проведем через эти точки вертикальные прямые. Отрезок  на оси у разобьем точками  на промежутки длины  и проведем через точки деления горизонтальные прямые. Таким образом, мы разобьем прямоугольник  на ячейки с горизонтальной стороной, меньшей  и вертикальной стороной  Сопоставим теперь каждой функции  ломаную  с вершинами в точках  т.е. в узлах построенной сетки и уклоняющуюся в точках  от функции  меньше, чем на  (существование такой ломаной очевидно).

Так как по построению

и

то

Так как между точками  и  функция  линейна, то

Пусть теперь х — произвольная точка отрезка [а, b] и  — ближайшая к х слева из выбранных нами точек деления. Тогда

Следовательно, ломаные  по отношению к Ф образуют -сеть. Число их конечно (так как вообще через конечное число точек можно провести лишь конечное число ломаных); таким образом, Ф вполне ограничено. Теорема полностью доказана.