Определение и примеры метрических пространств, страница 16

С понятием компактности тесно связано понятие полной ограниченности, которое мы сейчас введем.

Пусть М — некоторое множество в метрическом пространстве R и  — некоторое положительное число. Множество А из R называется -сетью по отношению к М, если для любой точки  найдется хотя бы одна такая точка  что

Например, целочисленные точки образуют на плоскости — сеть. Множество М называется вполне ограниченным, если для него при любом  существует конечная -сеть. Ясно, что вполне ограниченное множество обязательно ограничено, так как, если для М найдется -сеть, состоящая из п точек, то диаметр множества М не превосходит  как показывает приводимый ниже пример 2, обратное, вообще говоря, неверно.

Часто бывает полезно следующее очевидное замечание: если множество М вполне ограничено, то его замыкание [М]также вполне ограничено. Из определения полной ограниченности сразу следует, что всякое вполне ограниченное метрическое пространство R сепарабельно. Действительно, построим для каждого п в R конечную -сеть. Сумма их по всем п представляет собой счетное всюду плотное в R множество.

Примеры. 1. Для подмножества n-мерного евклидова пространства полная ограниченность совпадает с просто ограниченностью, т. е. с возможностью заключить данное множество внутрь некоторого достаточно боль-того куба. Действительно, если такой куб разбить на кубики с ребром то вершины этих кубиков будут образовывать конечную -сеть в исходном кубе, а значит и в любом множестве, лежащем внутри этого куба.

2. Единичная сфера S в пространстве l₂ представляет собой пример множества ограниченного, но не вполне ограниченного. Действительно, рассмотрим в S точки вида

Расстояние между любыми двумя такими точками  и  равно  Отсюда видно, что в S не может быть конечной -сети ни при каком

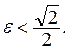
3. Рассмотрим в l₂множество П точек

удовлетворяющих следующим условиям:

Это множество называется фундаментальным параллелепипедом пространства l₂. Оно представляет собой пример бесконечномерного вполне ограниченного множества. Для доказательства его полной ограниченности поступим следующим образом.

Пусть  задано. Выберем п так, что  Каждой точке

                                                      (1)

из П сопоставим точку

                                                  (2)

из того же множества. При этом

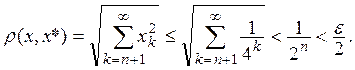
Множество П* точек вида (2) из П вполне ограничено (так как оно представляет собой ограниченное множество в n-мерном пространстве). Выберем в П* конечную -сеть. Ясно, что она будет в то же время -сетью во всем П.

Следующая теорема устанавливает связь между понятиями компактности, полноты и полной ограниченности.

Теорема 1. Для того чтобы множество М, лежащее в полном метрическом пространстве R, было компактно, необходимо и достаточно, чтобы М было вполне ограничено.

Доказательство. Необходимость. Предположим, что М не вполне ограничено, т. е. предположим, что для некоторого  в М нет конечной -сети. Возьмем в М произвольную точку  Так как, по предположению, в М нет конечной -сети, то найдется такая точка  что Далее, существует такая точка  что  и  (иначе точки  и  образовывали бы -сеть в М) и т. д., продолжая этот процесс, мы построим последовательность

точек из R, удовлетворяющих условию

Ясно, что из такой последовательности нельзя выбрать никакой сходящейся подпоследовательности.

Достаточность. Пусть R полно и М вполне ограничено. Докажем, что в М из всякой последовательности можно выбрать сходящуюся подпоследовательность. Пусть  — последовательность точек из М. Положим,

и построим для каждого  в М соответствующую конечную -сеть:

Опишем вокруг каждой из точек, образующих 1-сеть в М, сферу радиуса 1. Так как эти сферы покрывают все М, а число их конечно, то по крайней мере одна из них, назовем ее  содержит некоторую бесконечную подпоследовательность  последовательности  Далее, вокруг каждой из точек, образующих -сеть в R, опишем сферу радиуса  Так как число этих сфер опять-таки конечно, то по крайней мере одна из них, назовем ее  содержит бесконечную подпоследовательность  последовательности  Далее, найдем сферу  радиуса  содержащую бесконечную подпоследовательность  последовательности  и т. д.