Определение и примеры метрических пространств, страница 23

в метрическое пространство R. Когда t «пробегает» отрезок от а до b, то соответствующая точка Р «пробегает» некоторую «непрерывную кривую» в пространстве R. Нам предстоит дать строгие определения, связанные с изложенной сейчас грубо идеей. Порядок, в котором проходятся точки кривой, мы будем считать существенным свойством самой кривой. Одно и то же множество, изображенное на рис. 11, проходимое в направлениях, указанных на рис. 12 и 13, мы будем считать различными кривыми. В виде другого примера рассмотрим действительную функцию, определенную на отрезке [0, 1], которая изображена на рис. 14. Она определяет «кривую», расположенную на отрезке [0, 1] оси у, отличную от этого отрезка, однократно пройденного от точки 0 до точки 1, так как отрезок [А, В] проходится трижды (два раза вверх и один раз вниз).

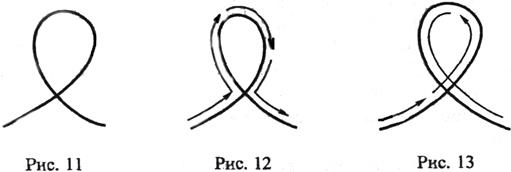
Однако при одинаковом порядке прохождения точек пространства выбор «параметра» t мы будем считать несущественным. Например, функции, изображенные на рис. 14 и 15 определяют одну и ту же «кривую», расположенную на оси у хотя значения параметра t, соответствующие какой-либо точке кривой, в случаях 14 и 15 могут быть различны. Например, в случае 14 точке А соответствуют на оси t две изолированные точки, а в случае 15 ей соответствует на оси t одна изолированная точка и лежащий правее отрезок (когда t пробегает этот отрезок, точка на кривой остается на месте)[11].

Переходим к формальным определениям. Две непрерывные функции

определенные соответственно на отрезках

называются эквивалентными, если существуют две непрерывные неубывающие функции

определенные на некотором отрезке

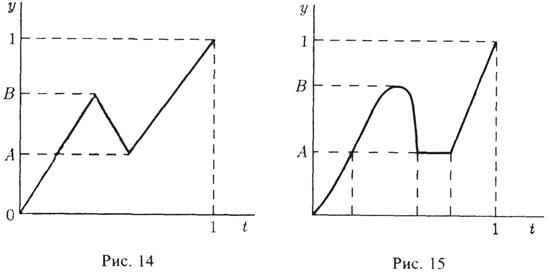
и обладающие свойствами

для всех

Легко видеть, что свойство эквивалентности рефлексивно (f эквивалентно f), симметрично (если  эквивалентно , то  эквивалентно ) и транзитивно (из эквивалентности  и  и эквивалентности  и  вытекает эквивалентность  и ). Поэтому все непрерывные функции рассматриваемого типа разбиваются на классы функций, эквивалентных между собой. Каждый такой класс и определяет непрерывную кривую в пространстве R.

Легко видеть, что для любой функции  определенной на каком-либо отрезке  найдется эквивалентная ей функция, определенная на отрезке

Для этого достаточно положить[12]

Таким образом, все кривые можно предполагать заданными параметрически при помощи функций, определенных на отрезке [0, 1].

Поэтому целесообразно ввести в рассмотрение пространство  непрерывных отображений отрезка I = [0, 1] в пространство R с метрикой

Будем считать, что последовательность кривых  сходится к кривой L, если кривые  можно параметрически представить в виде

а кривую L в виде

так, что

Применив обобщенную теорему Арцела (теорема 7 § 18) к пространству  получим теорему 1.

Теорема 1. Если последовательность кривых  лежащих в компакте К, можно представать параметрически при помощи равностепенно непрерывных функций на отрезке [0, 1], то из нее можно выделить сходящуюся подпоследовательность.

Определим теперь длину кривой, заданной параметрически функцией

как верхнюю грань сумм вида

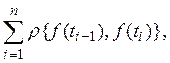
где точки  подчинены лишь условиям

Легко видеть, что длина кривой не зависит от выбора ее параметрического представления. Если ограничиться параметрическими представлениями посредством функций, заданных на отрезке [0, 1], то подобно рассмотрениям предшествующего параграфа легко доказать, что длина кривой есть полунепрерывный снизу функционал от f (в пространство ). На геометрическом языке этот результат можно выразить в виде такой теоремы о полунепрерывности.

Теорема 2. Если последовательность кривых  сходится к кривой L, то длина L не больше нижнего предела длин

Рассмотрим теперь специально кривые конечной длины. Пусть кривая определена параметрически функцией

Функция f, рассматриваемая лишь на отрезке [а, Т], где  определяет «начальный отрезок» кривой от точки

до точки

Пусть

его длина. Легко устанавливается, что

есть новое параметрическое представление той же кривой. При этом s пробегает отрезок