Определение и примеры метрических пространств, страница 8

(6) Хотя многие основные понятия переносятся с метрических пространств на топологические пространства, определенные в (4), в ряде случаев это понятие оказывается слишком общим. Важнейшим частным случаем топологических пространств являются те пространства, в которых наряду с аксиомами 1° и 2° выполняется еще так называемая аксиома отделимости Хаусдорфа:

3°. Любые две различные точки хну пространства Т имеют непересекающиеся окрестности.

Топологическое пространство, удовлетворяющее этой аксиоме, называется Хаусдорфовым топологическим пространством. Очевидно, что всякое метрическое пространство является Хаусдорфовым. Пространство, указанное в примере (4-6), не удовлетворяет аксиоме Хаусдорфа.

§11. Открытые и замкнутые множества на прямой

Структура открытых и замкнутых множеств в произвольном метрическом пространстве может быть весьма сложной. Мы рассмотрим сейчас простейший частный случай, а именно — открытые и замкнутые множества на прямой. В этом случае их полное описание не представляет большого труда и дается следующей теоремой.

Теорема 1. Всякое открытое множество на числовой прямой представляет собой сумму конечного или счетного числа попарно непересекающихся интервалов[4].

Доказательство. Пусть G — открытое множество и  Тогда, по определению открытого множества, найдется некоторый интервал I, содержащий точку х и целиком принадлежащий множеству G. Этот интервал можно всегда выбрать так, чтобы его концы были рациональными. Взяв для каждой точки  соответствующий интервал I, мы получим покрытие множества G счетной системой интервалов (эта система счетна, так как множество всех интервалов с рациональными концами счетно). Далее мы скажем, что интервалы I' и I" (из нашего покрытия) принадлежат одному классу, если существует такая соединяющая их конечная цепочка интервалов:

(принадлежащих нашему покрытию), что  пересекается с  Ясно, что таких классов будет конечное или счетное число. Далее, объединение всех интервалов, принадлежащих одному и тому же классу, представляет собой, очевидно, опять-таки некоторый интервал U, и интервалы, соответствующие различным классам, не пересекаются. Теорема доказана.

Так как замкнутые множества — это дополнения открытых, то отсюда следует, что всякое замкнутое множество на прямой получается выбрасыванием из прямой конечного или счетного числа интервалов.

Простейшие примеры замкнутых множеств — отрезки, отдельные точки и суммы конечного числа таких множеств. Рассмотрим более сложный пример замкнутого множества на прямой, так называемое канторово множество.

Пусть  — отрезок [0, 1]. Выбросим из него интервал  и оставшееся замкнутое множество обозначим

Затем выбросим из  интервалы  и  и оставшееся замкнутое множество (состоящее из четырех отрезков) обозначим  В каждом из этих четырех отрезков выбросим средний интервал длины  и т. д. Продолжая этот процесс, получим убывающую последовательность замкнутых множеств  Положим,

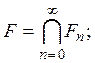
F — замкнутое множество (как пересечение замкнутых). Оно получается из отрезка [0, 1] выбрасыванием счетного числа интервалов. Рассмотрим структуру множества F. Ему принадлежат, очевидно, точки

                                                 (1)

концы выбрасываемых интервалов. Однако множество F не исчерпывается этими точками. Действительно, те точки отрезка [0, 1], которые входят в множество F, можно охарактеризовать следующим образом. Запишем каждое из чисел  по троичной системе:

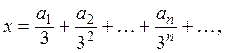
где числа  могут принимать значения 0, 1 и 2. Как и в случае обычных десятичных дробей, некоторые числа допускают двоякую запись. Например,

Легко проверить, что множеству F принадлежат те и только те числа  которые могут быть записаны, хотя бы одним способом, в виде троичной дроби так, чтобы в последовательности  единица ни разу не встречалась. Таким образом каждой точке  можно поставить в соответствие последовательность

                                                    (2)