Определение и примеры метрических пространств, страница 21

Пусть функция  выбрана так, что  Тогда

если i выбрано так, что

Отсюда вытекает, что  и, таким образом, компактность D в  а следовательно, и в  доказана.

§ 19. Действительные функции на метрических пространствах

Действительной функцией на пространстве R называется отображение R в пространство  (действительную прямую).

Так, например, отображение в  есть обычная действительная функция от п переменных.

В случае, если пространство R само состоит из функций, то функции от элементов R обычно называются функционалами. Приведем несколько примеров функционалов от функций f(x), определенных на сегменте [0, 1]:

а функция  определена для всех действительных

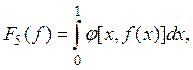
где  определена и непрерывна для всех и всех действительных у;

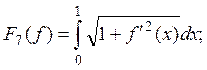
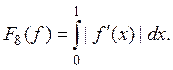
Функционалы могут быть определены на всем R или на его подмножестве. Например, в пространстве С функционалы,  определены на всем пространстве,  определен лишь для функций, дифференцируемых в точке  — Для функций с интегрируемым  — для функций с интегрируемым |f ' (x)|.

Определение непрерывности для действительных функций и функционалов остается тем же, что и для всех отображений вообще (см. § 12).

Например, в С  есть непрерывный функционал, так как

 — также непрерывные функционалы в С;  непрерывен в пространстве С, если функция  непрерывна по всем аргументам;  в пространстве С разрывен в любой точке, где он определен. Действительно, пусть g(х) таково, что  и  и  Тогда  а  Этот же функционал непрерывен в пространстве  функций, имеющих непрерывную производную, с метрикой,

 есть также разрывный функционал в пространстве С. Действительно, пусть  и  Тогда  но в то же время  есть постоянная (не зависящая от n), большая чем a

Таким образом,  не стремится к

Следовательно,  разрывен в точке

В силу того же примера  также разрывен в пространстве С. В пространстве  оба функционала  и  непрерывны.

Для действительных функций на компактах имеют место следующие теоремы, являющиеся обобщением хорошо известных теорем элементарного курса анализа:

Теорема 1. Непрерывная действительная функция на компакте равномерно непрерывна.

Доказательство. Пусть f непрерывна, но не равномерно непрерывна, т. е. существуют  и  такие, что

Из последовательности  можно, выбрать подпоследовательность  сходящуюся к х. Тогда и  и либо  либо  что противоречит непрерывности f(x).

Теорема 2. Непрерывная на компакте функция ограничена на нем.

Доказательство. Если бы f была неограниченной, то существовала бы такая последовательность  что

Выбираем из  сходящуюся подпоследовательность  Тогда в сколь угодно малой окрестности х функция f(x) будет принимать сколь угодно большие значения, что противоречит непрерывности.

Теорема 3. Непрерывная на компакте функция достигает на нем своей верхней и нижней грани.

Доказательство. Пусть  Тогда существует такая последовательность  что

Выбираем из  сходящуюся подпоследовательность  По непрерывности f(x) = А. Для  доказательство вполне аналогично.

Теоремы 2 и 3 допускают обобщение и на более широкий класс функций (так называемые полунепрерывные функции).

Функция f(х) называется полунепрерывной снизу (сверху) в точке  если для любого  существует -окрестность  в которой

Например, функция «целая часть от х»,  полунепрерывна сверху. Если увеличить, (уменьшить) значение  непрерывной функции в какой-либо одной точке  то мы получим полунепрерывную сверху (снизу) функцию. Если f(х) полунепрерывна сверху, то — f(х) полунепрерывна снизу. Эти два замечания позволяют сразу построить большое число примеров полунепрерывных функций.

Будем рассматривать также функции, допускающие значения  Если  то f(х) будем считать полунепрерывной снизу в  и полунепрерывной сверху в  если для любого h > 0 имеется окрестность  в которой

Если  то f(х) будем считать полунепрерывной сверху в  и полунепрерывной снизу в  если для любого h > 0 имеется окрестность точки  в которой