Определение и примеры метрических пространств, страница 15

Докажем, что тогда на некотором сегменте  существует одна и только одна система решений  удовлетворяющих системе (4) и начальным условиям (5).

Система (4) вместе с начальными условиями (5) эквивалентна системе интегральных уравнений

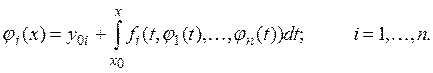                         (6)

В силу непрерывности функций  в некоторой области  содержащей точку  выполнены неравенства  где K — некоторое постоянное число.

Подберем теперь d > 0 так, чтобы выполнялись условия:

1)  если

2)

Рассмотрим теперь пространство  элементами которого являются упорядоченные системы  состоящие из п функций, определенных и непрерывных для всех х при  и таких, что  с метрикой

Отображение  задаваемое системой интегральных уравнений

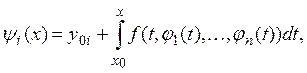
есть сжатое отображение полного пространства  в себя. Действительно,

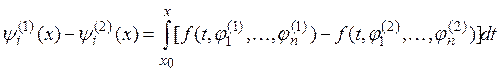
и, следовательно,

Так как Md < 1, то А есть сжатое отображение.

Отсюда вытекает, что операторное уравнение  имеет одно и только одно решение.

III. Применим теперь метод сжатых отображений для доказательства существования и единственности решения неоднородного линейного интегрального уравнения Фредгольма второго рода:

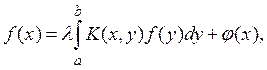                                        (7)

где K(х, у) (так называемое ядро) и  есть данные функции, f(x) — искомая функция, а  — произвольный параметр.

Мы увидим, что наш метод применим лишь в случае достаточно малых значений параметра

Предположим, что  и  непрерывны при   и, следовательно,  Рассмотрим отображение  т. е. 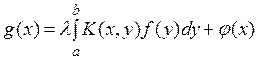 полного пространства  в себя. Получаем:

Следовательно, при  —- отображение А является сжатым.

Отсюда на основании принципа сжатых отображений можем заключить, что для всякого  уравнение Фредгольма имеет единственное непрерывное решение. Последовательные приближения к этому решению:  имеют вид:

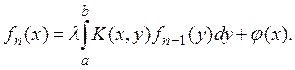
В качестве  можно взять любую непрерывную функцию.

IV. Этот метод применим и в случае нелинейных уравнений вида

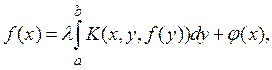                                      (8)

где K и  непрерывны и, кроме того, K удовлетворяет условию

при  так как и в этом случае для отображения  полного пространства  в себя, заданного формулой

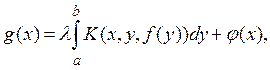
имеет место неравенство

V. Рассмотрим интегральное уравнение типа Вольтерра

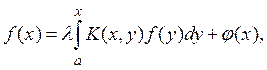                                           (9)

отличающееся от уравнения типа Фредгольма тем, что верхний предел в интеграле — переменная величина х. Это уравнение можно рассматривать как частный случай уравнения Фредгольма, доопределив функцию K(х, у)при у > х равенством

В отличие от интегрального уравнения Фредгольма, где мы были вынуждены ограничиться малыми значениями параметра  к уравнениям Вольтерра принцип сжатых отображений (и основанный на нем метод последовательных приближений) применим при всех значениях параметра  Заметим, прежде всего, что принцип сжатых отображений может быть обобщен следующим образом:

если А — такое непрерывное отображение полного метрического пространства R в себя, что отображение  при некотором п является сжатым, то уравнение

Ах = х

имеет одно и только одно решение.

Действительно, взяв произвольную точку  рассмотрим последовательность  Повторяя рассуждения, проведенные в § 14, получаем, что эта последовательность сходится. Пусть

Тогда

Действительно,

Так как отображение  — сжатое, то

Следовательно,

т. е.

Рассмотрим теперь отображение

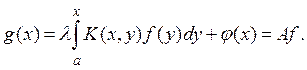
Если  и  — две непрерывные функции на отрезке [а, b], то

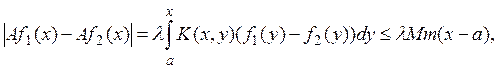
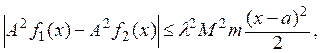
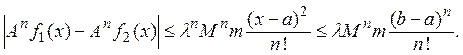
При любом значении  число п можно выбрать настолько большим, что

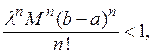
т. е. отображение  будет сжатым. Следовательно, уравнение Вольтерра (9) при любом  имеет решение, притом единственное.

§ 16. Компактные множества в метрических пространствах

Множество М в метрическом пространстве R называется компактным, если из всякой последовательности его элементов можно выбрать подпоследовательность, сходящуюся к некоторому

Так, например, в силу теоремы Больцано-Вейерштрасса, всякое ограниченное множество на числовой прямой компактно. Другие примеры компактных множеств будут указаны ниже. Очевидно, что любое подмножество компактного множества также компактно.